并行埋地敷设管道安全性影响评估技术研究
来源: 作者: 时间:2018-7-12 阅读:
董绍华 彭东华 邸鑫 张河苇
中国石油大学(北京)
摘要:管道运输系统是现代重要的运输系统之一,已经普遍应用于现代工业生产、城市建设以及社会各个领域。管道运输是陆地输送天然气主要方式。我国中西部地区地形复杂,管道走廊用地紧张,多条管道不可避免的需要并行敷设,而且在以后的管道建设中,并行敷设管段还要增加,因此就,解决并行管道建设、生产运行等方面面临的问题,及时开展风险评价是非常必要。本文通过对管道泄漏工况的分析,模拟管道爆炸初始TNT爆炸当量,采用ANSYS -Autodyn软件对管道爆炸冲击进行数值模拟,结合1016mm管道敷设工况,确定物理模型参数,分析不同并行间距下埋地天然气爆炸对并行管道的冲击破坏效应,提出并行管道安全间距,确定其合理范围,同时评价一条管道发生失效时对另一条管道的影响,通过并行管道的安全评价,可为管道运营和维护提供有力的帮助。
关键词:天然气管道 并行 风险 评估 模型
1、前言
管道敷设方式一般采取单根管道埋地的独立敷设方式,但随着经济发展和地理环境的限制,路由紧张局面必须采取并行敷设和同沟敷设,国外俄罗斯长输油气管道采取并行的工程实例较多,其中有著名的俄罗斯中亚-中央输气管道,一线建于1967年,到1976年,四线建成。中亚-中央输气管道主要有四条,主要负责莫斯科的天然气输送。线路平均长度达到2800多公里[1]。
近年来,我国探明天然气储量持续增长。因天然气是一次性能源中相对清洁的产品,消费规模也迅速扩大。新增探明储量主要位于鄂尔多斯、塔里木、准噶尔盆地及四川盆地。管道敷设也从单根管线发展到多条管线并行敷设、联合运行的局面。陕京二线和三线并行段达到460公里以上,途径很多地形复杂区域,有的地段间距不足5米,具有极高的施工难度和巡线难度。
中亚输气管道并行敷设,两管直径均为1067mm,管线经过土库曼-乌兹别克斯坦-哈萨克斯坦后到达中国边境霍尔果斯,目前该项目正在实施中,线路全长为1818km。
除此以外,输油管道也有并行敷设的情况。例如,目前西气东输二线在新疆、甘肃和宁夏境内分别与已建的独鄯成品油管道、西部管道和西气东输一线长距离并行敷设,同时还要考虑与正在规划的独乌鄯原油管道,鄯乌输气管道,西气东输三线等管道并行。此外,庆铁线与庆铁复线(八三管道)也是并行敷设,管道起点为大庆市林源,终点为铁岭输油站,全长516.34km。
埋地管道不同于地上管道,其发生失效后泄漏引发管道爆炸的几率远低于地上管道。但由于土壤对爆炸空间的限定,埋地管道发生爆炸后,爆轰现象形成的冲击波受到土壤持续反射作用,冲击波超压迅速上升,比地上管道爆炸的产生的冲击波超压高一个数量级。但由于土壤对冲击波压力和冲量的传递比空气慢,因此冲击波对并行管线的破坏是一个缓慢的过程。随着并行间距的增加,爆炸能量逐渐被土壤吸收,冲击波对并行管线的破坏能力也迅速下降。因此,埋地管道爆炸与地上管道爆炸相比,其对并行管线的破坏程度、作用时间、变形规律存在很大差异。
国内有关设计标准规定了管道并行间距为6米[1-2],并行管道的间距是否符合风险后果的要求,需要建立分析模型和力学仿真得到。
本文采用有限元仿真模拟的方法,基于管土作用的TNT爆炸当量爆破冲击能量守恒原理,合理确定边界,解决并行管道安全间距问题,建立了量化有限元模型,使用现代爆炸力学大型有限元分析系统仿真技术,确定并行管道间距的合理范围,同时评价一条管道发生失效时对另一条管道的影响,通过并行管道的的定量化安全评价,可为管道的安全运营和入场维护提供技术支持。
2 并行管道数学模型
2.1 有限元模型
采用Autodyn软件对管道爆炸冲击进行数值模拟。结合1016mm管道敷设工况,确定物理模型参数,分析不同并行间距下埋地天然气爆炸对并行管道的冲击破坏效应。
管道泄漏时间取![]() =180s,转化为TNT当量
=180s,转化为TNT当量![]() =25.74kg。初始化TNT当量球,取半径156mm。建立二维楔形TNT爆炸模型:156mm
=25.74kg。初始化TNT当量球,取半径156mm。建立二维楔形TNT爆炸模型:156mm![]() 1000mm,计算时间0.25ms。空气材料Air(Ideal gas),管线材料Steel1006和Steel4340和,TNT材料状态方程JWL,土壤材料选用CONC-35MPA,其状态方程为P-alpha,强度模型为RHT-concrete,GAS材料基于AIR材料本构模型修改密度和内能。
1000mm,计算时间0.25ms。空气材料Air(Ideal gas),管线材料Steel1006和Steel4340和,TNT材料状态方程JWL,土壤材料选用CONC-35MPA,其状态方程为P-alpha,强度模型为RHT-concrete,GAS材料基于AIR材料本构模型修改密度和内能。
总体物理模型设置为:两个内径1197mm的管道并行放置在土壤中,埋深![]() =1.5m。土壤除顶部与空气接触外,其余5面默认为无限边界。两个管道与土壤水平方向的边界距离均保持
=1.5m。土壤除顶部与空气接触外,其余5面默认为无限边界。两个管道与土壤水平方向的边界距离均保持![]() =2m。两管道中心间距
=2m。两管道中心间距![]() 分别设置为2m、3m、4m、5m、6m、7m、8m,其中一个管道以等当量TNT球代替,见图2.1。
分别设置为2m、3m、4m、5m、6m、7m、8m,其中一个管道以等当量TNT球代替,见图2.1。
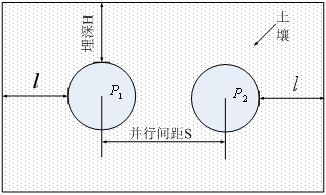
图2.1 物理模型示意图
为提高计算效率,选取建立1/2管道、1/2土壤和1/4TNT球物理模型。在Workbench中建立(4m+![]() )
)![]() 2m
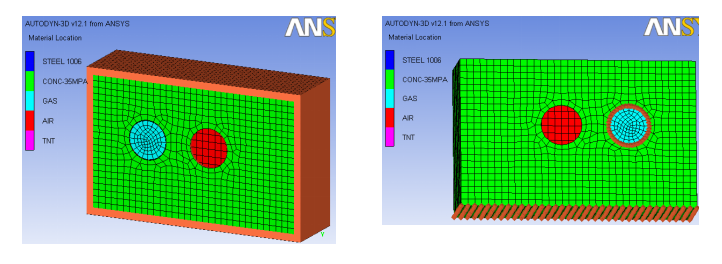
2m![]() 2m的土壤模型,并在管道位置预留两个圆柱孔洞。建立Pipeline模型和Gas模型,填充进土壤圆柱孔洞中,设置接触对。
2m的土壤模型,并在管道位置预留两个圆柱孔洞。建立Pipeline模型和Gas模型,填充进土壤圆柱孔洞中,设置接触对。

图2.2 workbench埋地管道模型
将上述空间模型通过Explicit Dynamics模块导入Autodyn软件,确定Grid、Ini.Cond条件和边界条件,修正GAS材料状态方程参数和强度模型参数。添加Air和TNT材料,建立Space的Euler-FCT模型,覆盖整体土壤模型。将计算后的二维楔形TNT爆炸模型remap导入Space模型。球心坐标选取原爆破并行管线的轴心。

图2.3 空间模型示意图
2.2 边界条件及接触
土壤模型除地表表面外,其余5面为半无限体,均设置为Flow out边界。土壤地面添加![]() =0m/s约束。管道内压为6MPa,
=0m/s约束。管道内压为6MPa,![]() =0端轴向位移
=0端轴向位移![]() =0m/s,见图2.4。
=0m/s,见图2.4。
接触对的设置同时考虑管道内部与Gas、外部与空气的接触。此处设置内部接触对为trajectory接触,保证能量守恒和动量守恒,并随时跟踪模型中节点与面的接触。设置外部接触为流固耦合,保证能量传递的准确性。
为跟踪管道管壁位移量和速度大小随时间变化的关系,需要在管道模型上添加一定数量的Gauge点,其位置极坐标以![]() 轴为原点,每隔45°选取一系列Gauge点,见图2.5。
轴为原点,每隔45°选取一系列Gauge点,见图2.5。

3 计算结果分析
由于埋地管道同时受管道爆炸和土壤变形挤压作用,容易产生大变形破坏甚至出现管道压裂现象。因此对埋地管道的失效分析不同于地上管道,须根据管道的被破坏形式分为压裂失效和大变形破坏两大部分。下面分别展示并行间距2m、3m、4m、5m、6m、7m、8m的埋地管道受爆炸冲击的最终计算结果,分别探讨其破坏规律。
3.1 并行间距2m
该物理模型中的gauge点分布如下图所示,
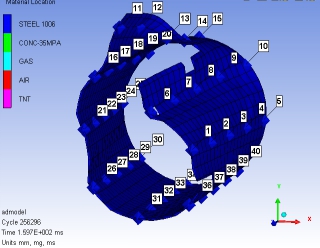
图3.1 2m并行间距管道Gauge点分布图
各系列Gauge点随时间推移所受冲击压强及积分变化变化曲线图见图3.2。总计算时间为160ms。埋地管道发生爆炸时,近爆炸源土壤发生液化现象,冲击超压直接透过土壤传递给近距离并行管线,管道同时受爆炸超压和土壤塑性变作用,发生大变形甚至破裂失效。
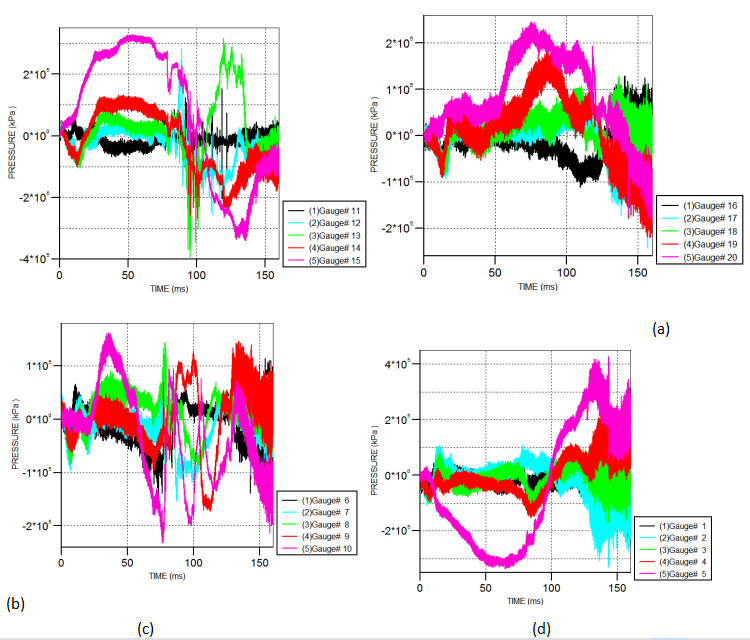
图3.2 2m并行间距各系列Gauge点压强曲线图
由图3.2可看出,管道Z=0端所受冲击超压依旧大于管道Z=2m端,即管道远离爆炸源部位所受超压大于靠近爆炸源部位,这一点与地上管道一致,均是由冲击波在传递过程中发生折射、振荡造成的。
系列Gauge点中均以管道尾端Gauge点所受压强最大,且振荡最明显。故表1数值只用来代表各系列Gauge点所受冲击压强数量级,具体数值只做参考.
表1 Gauge点所受冲击压强超压最值表
|
Gauge点 |
1~5 |
6~10 |
11~15 |
16~20 |
21~25 |
26~30 |
31~35 |
36~40 |
|
正超压(MPa) |
425.9 |
162.2 |
327.4 |
245.6 |
354.0 |
245.2 |
156.2 |
243.3 |
|
负超压(MPa) |
-338.1 |
-231.5 |
-392.7 |
-243.6 |
-282.3 |
-391.8 |
-211.8 |
-218.1 |
表2 Gauge点总位移最大值
|
Gauge点 |
1~5 |
6~10 |
11~15 |
16~20 |
21~25 |
26~30 |
31~35 |
36~40 |
|
总位移(mm) |
257.4 |
526.8 |
461.3 |
107.5 |
108.2 |
155.0 |
243.0 |
365.8 |
表3.2中,Gauge点6的位移达527mm,为管道变形最大点,管道第二大变形位置为管道正面靠近顶部的部位,即与管道正对爆炸源位置呈逆时针45°夹角处。管道背面变形量整体小于正面变形量,最大值仅为155mm。管道受冲击载荷状况见下图3.3。

图3.3 管道受冲击变形过程
当埋地管道并行间距为2m时,管道爆炸对并行管道的冲击破坏效应是巨大的,会迅速引起管道破裂失效。其变形原理为:爆炸源产生的高强度冲击波对周边土壤产生振动液化,形成爆破漏斗。土壤持续受振动冲击产生塑性变形,该变形延伸至并行管线周围,对管道正面进行挤压,导致管道水平方向上继续大幅变形。管道背面土壤受漏斗挤压密度增大,结构趋于稳定,导致管道背面变形远小于正面,最终引起管道破裂。变形规律为:管道起始变形位置为正面Gauge点1~5部位,之后该部位持续凹陷。管道顶部和底部不断向外延伸,管道背面受土壤作用不发生大形变。最终管道呈被压裂状态,破裂位置为管道顶部和底部,与最大变形位置相垂直。
3.2 并行间距3m
该物理模型中的gauge点分布如下图所示,其详细位置坐标见附录P。
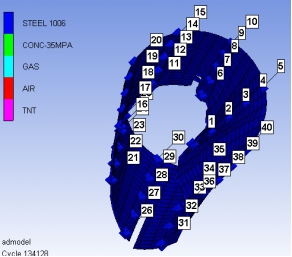
图3.4 3m并行间距管道Gauge点分布图
各系列Gauge点随时间推移所受冲击压强及积分变化变化曲线图见图3.4。由前面知,埋地管道受近距爆炸冲击产生实效现象的时间在100ms以内,这里选择计算时间为160ms。埋地管道发生爆炸时,近爆炸源土壤发生液化现象,冲击超压直接透过土壤传递给近距离并行管线,管道同时受爆炸超压和土壤塑性变作用,发生大变形甚至破裂失效。
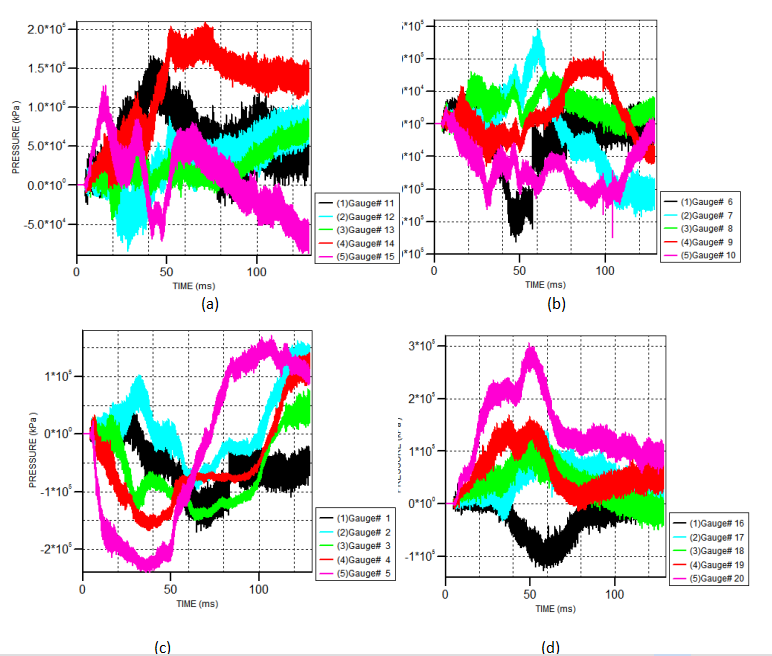
图3.5 3m并行间距各系列Gauge点压强曲线图
图3.5 中管道远离爆炸源部位所受超压大于靠近爆炸源部位,系列Gauge点中均以管道尾端Gauge点所受压强最大,且振荡最明显,不能代表引起管道大变形的实际超压值,这里只选取Z=2m端即近爆炸源端的Gauge点分析。下表为各Gauge points系列起始点的超压最值表。
|
Gauge点 |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
|
正超压(MPa) |
46.6 |
48.4 |
165.8 |
41.2 |
33.7 |
58.2 |
93.8 |
39.1 |
|
负超压(MPa) |
-170.7 |
-181.7 |
-264.1 |
-127.8 |
-163.7 |
-204.5 |
-119.0 |
-253.3 |
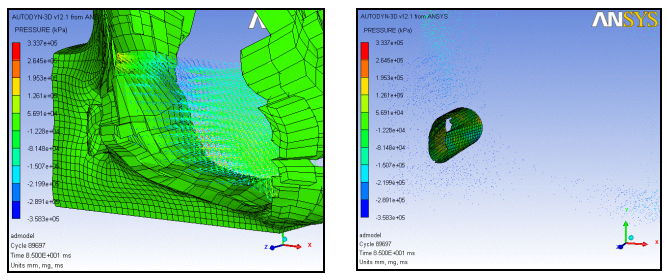
图3.6 管道受冲击变形过程
图3.6所示,管道破裂位置与前面理论位置一致。说明埋地管道并行间距为3m时,管道爆炸虽然不能对并行管线产生直接的超压破坏,但爆炸引起的周围土壤塑性变形会直接挤压管道引起管道整体沿X轴方向移动,管道正面变形量远大于管道背面,导致管道正面斜上、斜下部位为相对变形量最大部位,为管道破裂位置。而管道正对爆炸源位置为管道最大变形,但不是管道破裂失效位置。
总体来看,并行间距为3m时,埋地管道受并行管线爆炸冲击所受到的冲击破坏效应与2m并行间距基本一致,其失效位置均为管道正面靠近顶部和底部的部位,其失效原因均由土壤塑性变形对管道产生挤压引起。管道最大变形均为正对爆炸源位置,失效位置与最大变形位置呈90°垂直。地下爆炸虽然促使土壤形成爆破漏斗,但由于并行间距小,漏斗不能在管道位置形成集中堆积应力,管道变形呈整体X轴负方向移动。
3.3 并行间距4m~6m
埋地管道同时受管道爆炸和土壤变形挤压作用,容易产生大变形破坏甚至出现管道压裂现象。因此对埋地管道的失效分析不同于地上管道,须根据管道的被破坏形式分为压裂失效和大变形破坏两大部分。前面通过对2m、3m并行间距系列进行分析,确定在并行间距小于3m时埋地管道爆炸会造成并行管道破裂失效。本文的最终计算目的是确定管道失效后果风险分析,而管道受爆炸破坏会发生失效破裂和大变形破坏两种风险后果。
下图分别展示埋地管道间距4-6米的管道受爆炸冲击破坏形态的最终计算结果,并与间距7-8米的破坏形态计算结果相比较,根据计算结果,以不同的破坏形式对并行间距进行划分,分别探讨其破坏规律(在下一节中不再对7-8米间距的破坏形态图进行分析和说明)。
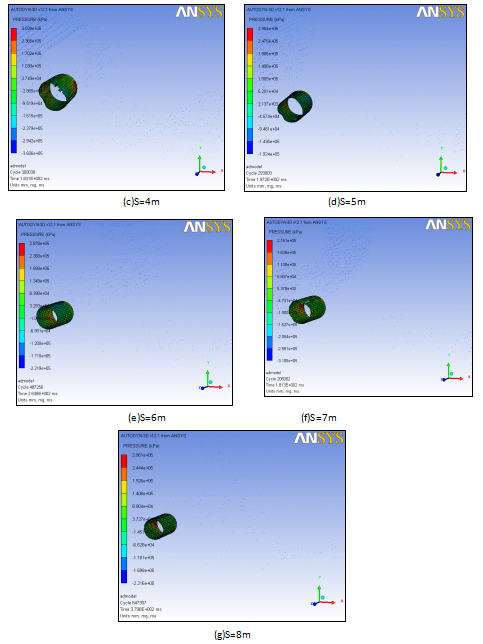
图3.7 不同并行间距下管道最终变形
图3.7 中![]() 为并行间距。由图可看出,并行间距在2m-3m之间时,管道受土壤水平变形挤压,管道顶部和底部发生压裂失效。并行间距在4m-6m之间时,管线爆炸产生的冲击波无法直接对并行管线产生破坏,而是掀起土壤形成爆破漏斗,爆破漏斗在颈部形成土壤堆积,使土壤产生塑性变形,对管道产生挤压作用,导致管道发生压裂失效。并行间距达到7m后,土壤即使形成爆破漏斗,由于并行间距大,漏斗产生的土壤堆积也无法直接作用并行管线,这时管线的变形主要由周围土壤的弹性变形力造成。这里的理论前提是将远端的土壤看做粘弹性线性变形,该理论前面已详细阐述,这里不再赘述。
为并行间距。由图可看出,并行间距在2m-3m之间时,管道受土壤水平变形挤压,管道顶部和底部发生压裂失效。并行间距在4m-6m之间时,管线爆炸产生的冲击波无法直接对并行管线产生破坏,而是掀起土壤形成爆破漏斗,爆破漏斗在颈部形成土壤堆积,使土壤产生塑性变形,对管道产生挤压作用,导致管道发生压裂失效。并行间距达到7m后,土壤即使形成爆破漏斗,由于并行间距大,漏斗产生的土壤堆积也无法直接作用并行管线,这时管线的变形主要由周围土壤的弹性变形力造成。这里的理论前提是将远端的土壤看做粘弹性线性变形,该理论前面已详细阐述,这里不再赘述。
管道近爆炸源端变形量最大,因此取管道上各Gauge点系列的起始点位研究对象,绘制其压强和位移曲线,见图3.8。图中自左到右、自上到下依次为压强曲线图、位移曲线图、速度曲线图、冲量曲线图。
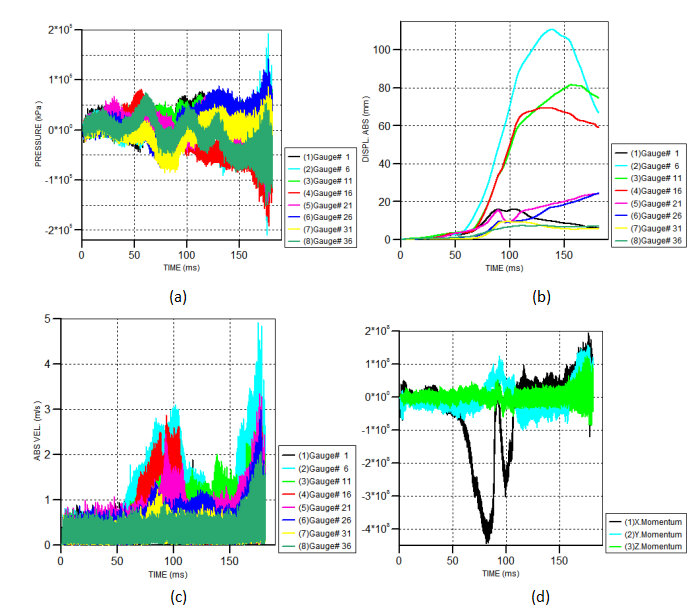
图3.8 6m并行间距各Gauge点参量曲线图
并行间距分别为4m、5m、6m时,其所受爆炸超压幅度和波动频率基本一致,Gauge点位移速度梯度下降,但仍保持同一数量级。管道受冲击冲量趋势一致,均在t=50-100ms内阶跃上升,管道变形量均在这一时间段内迅速上升。
各点最大位移值见表3.6、表3.7和表3.9。
表3.6 4m并行间距Gauge点位移最大值
|
Gauge点 |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
|
总位移(mm) |
91.65 |
296.92 |
154.26 |
171.74 |
73.74 |
66.28 |
11.18 |
16.37 |
|
Gauge点 |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
|
总位移(mm) |
12.46 |
51.78 |
23.19 |
30.51 |
37.15 |
99.64 |
14.64 |
9.93 |
表3.8 6m并行间距Gauge点位移最大值
|
Gauge点 |
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
|
总位移(mm) |
16.01 |
110.75 |
81.54 |
69.48 |
24.10 |
24.26 |
95.72 |
73.18 |
以6m并行间距系列为例,观察其整体变形过程,分析其变形规律。见图3.9,图中左边同时显示土壤、管道、Gas和冲击矢量,右边只显示管道和冲击矢量。
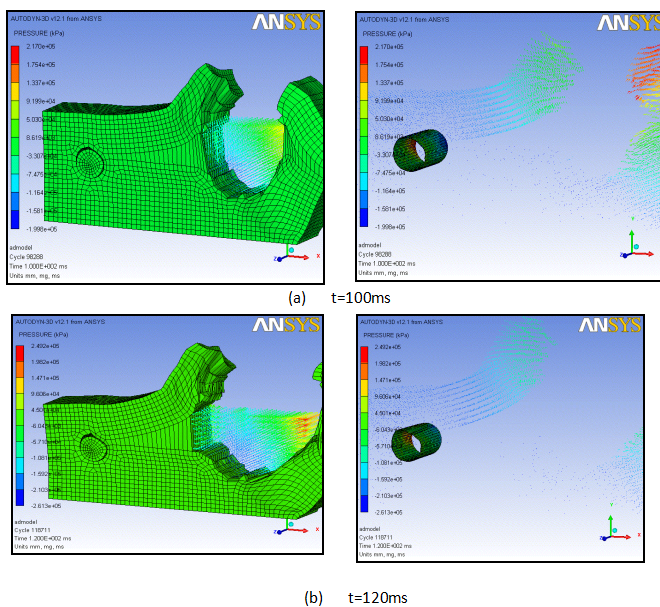
图3.9 管道变形过程
土壤边界条件设置为:除地表表面外,其余5面为无限边界。当![]() =50ms时,在爆炸冲击的不断振荡下,周边土壤不断液化凹陷,开始被向上掀起。图3.8中可看出,爆炸超压已无法直接作用于管道,管道在前50ms基本无形变。
=50ms时,在爆炸冲击的不断振荡下,周边土壤不断液化凹陷,开始被向上掀起。图3.8中可看出,爆炸超压已无法直接作用于管道,管道在前50ms基本无形变。
![]() =100ms时,土壤已形成爆破漏斗,被掀起的土壤向上弯曲,引起X轴负方向的土壤受挤压塑性变形,包括并行管道顶部的土壤。土壤塑性变形产生内部应力,压迫管道引起形变。
=100ms时,土壤已形成爆破漏斗,被掀起的土壤向上弯曲,引起X轴负方向的土壤受挤压塑性变形,包括并行管道顶部的土壤。土壤塑性变形产生内部应力,压迫管道引起形变。
![]() =120ms时,土壤持续变形,在Gauge点6处形成集中应力,造成管道破裂。在管道相对位置Gauge点31处,土壤受上下挤压变形,带动管道向内凹陷,管道变形值达95.72mm。
=120ms时,土壤持续变形,在Gauge点6处形成集中应力,造成管道破裂。在管道相对位置Gauge点31处,土壤受上下挤压变形,带动管道向内凹陷,管道变形值达95.72mm。
当120ms之后爆炸冲击波不断向地表扩散,总能量释放进空气中。但由于爆破漏斗形变速度小于爆轰波传递速度,冲击波释放完毕后,土壤仍然保持被掀起状态,引起管道持续变形。
以上即是并行间距6m系列埋地管道受爆炸冲击影响的破裂失效过程。4m系列和5m系列与之类似,不再赘述。
终上所述,并行间距为4m-6m时,埋地管道受并行管线爆炸冲击作用下,其变形和失效规律为:管道最大变形位置为管道正面靠近顶部处和背面靠近底部处,亦是管道破裂部位。其变形原因主要由土壤变形引起,具体过程与3m系列类似,爆炸冲击已无法对管道产生直接作用。爆炸能量释放进空气中后,管道受土壤挤压作用仍持续变形。
3.4 并行间距7m~8m
当并行间距![]() 8m时,管道不再产生破裂失效现象。这里从压力和变形量角度分析其受冲击破坏效应。
8m时,管道不再产生破裂失效现象。这里从压力和变形量角度分析其受冲击破坏效应。
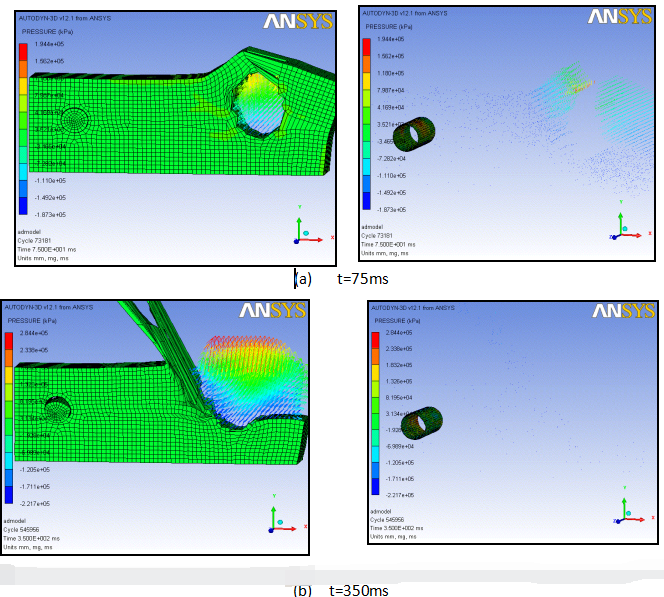
图3.10 管道变形过程
图3.1o为8m并行间距下管道变形过程。当t=80ms时,土壤开始形成爆破漏斗。之后,漏斗体积不断扩大,但由于最终漏斗口径是一定的,其形成的土壤堆积与并行管道仍存在很大距离,所以爆破漏斗不再对并行管线的变形起决定作用。之后,地表土壤不断被掀飞(图3.10),管道变形受土壤整体粘弹性变形作用,其大变形位置依然为管道正面靠顶部位置,但该变形量不会引起管道破裂失效。
综上,在并行间距大于等于8m时,管道不再发生破裂,其变形应力来自土壤粘弹性变形应力。最大变形位置为管道正面靠近顶部位置。虽然该变形量不会导致管道破裂,但已超出管道椭圆化设计准则。为保证埋地并行管道安全,其敷设间距应当大于等于8m。
4 模型有效性验证
TNT当量法为蒸气云爆炸(Unconfined Vapor Cloud Explosion ,简称UVCE)模拟方法中的典型模型,其原理是把气云爆炸的破坏作用转化成TNT爆炸的破坏作用,从而把蒸气云的量转化成TNT当量。
当埋地管道泄漏爆炸时,不考虑地表上已逸出可燃气体,在土壤所包含的气相进入饱和状态时,计算埋地管道的总泄漏量![]() 并转化为TNT当量
并转化为TNT当量![]() ,对埋地管道爆炸冲击能量进行预测。
,对埋地管道爆炸冲击能量进行预测。
![]() (4.1)
(4.1)
式中:
![]() ——蒸气云的TNT当量,kg;
——蒸气云的TNT当量,kg;
![]() ——蒸气云中燃料的总质量,kg;
——蒸气云中燃料的总质量,kg;
![]() ——蒸气云当量系数,统计平均值为0.04;
——蒸气云当量系数,统计平均值为0.04;
![]() ——蒸气的燃烧热,J/kg;
——蒸气的燃烧热,J/kg;
![]() ——TNT的爆炸热,J/kg,(4230~4836kJ/kg,一般取平均4500kJ/kg);
——TNT的爆炸热,J/kg,(4230~4836kJ/kg,一般取平均4500kJ/kg);
取泄漏时间![]() =180s,其他参数与地上管道设定一致,代入式(4.1)得
=180s,其他参数与地上管道设定一致,代入式(4.1)得![]() =1072.81kg,转化为TNT当量为
=1072.81kg,转化为TNT当量为![]() =25.74kg。
=25.74kg。
土壤中的爆炸冲击波波阵面峰值压力![]() 、比冲量
、比冲量![]() 和冲击波作用时间
和冲击波作用时间![]() 通过式(4.2)计算。冲击波波阵面峰值压力
通过式(4.2)计算。冲击波波阵面峰值压力![]() 、比冲量
、比冲量![]() 和冲击波作用时间
和冲击波作用时间![]() 与爆炸特征长度
与爆炸特征长度![]() 之间的关系见式(4.2)。
之间的关系见式(4.2)。
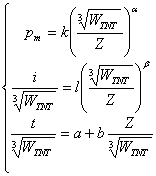 (4.2)
(4.2)
式中,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() 为TNT装药的试验常数。针对陕京二线埋地敷设管线土壤主要为天然气组合砂,这里取
为TNT装药的试验常数。针对陕京二线埋地敷设管线土壤主要为天然气组合砂,这里取![]() =230,
=230,![]() =2,
=2,![]() =1.10,
=1.10,![]() =0.075,
=0.075,![]() =0.004,
=0.004,![]() =0.016。
=0.016。
埋地管道不同于地上管道,当并行间距小于8m时,管道会发生破裂失效,且其变形应力来自土壤塑性变形应力作用,该数值无法用理论验证。当并行间距达到8m后,管道变形力来自土壤粘弹性,可直接计算其理论超压值。
将埋地管道爆炸的TNT当量值![]() =25.74kg代入式(4.2),得
=25.74kg代入式(4.2),得
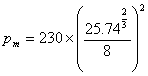 =273.12MPa
=273.12MPa
该值与Gauge点6所受正超压均值误差为:
![]() =21.23%
=21.23%
表明埋地管道爆炸模型建立合理,计算结果具备有效性。
5 结论
本文以埋地管道为研究对象,建立地下管道爆炸对并行管线的冲击模型,通过对不同间距系列管道变形分析,得到以下冲击破坏规律:
(1)在并行间距不大于3m时,埋地管道变形前期受爆炸冲击超压影响,后期主要由土壤变形挤压造成。管道正面全部受土壤挤压产生大变形,管道正面集体向X轴负方向移动,管道相对变形量最大点为管道顶部和底部,导致这两个部位发生破裂。
(2)并行间距为4m-6m时,埋地管道的变形原因主要由土壤变形引起,具体过程与3m系列类似,爆炸冲击已无法对管道产生直接作用。管道最大变形位置为管道正面靠近顶部处和背面靠近底部处,亦是管道破裂部位。爆炸能量释放进空气中后,管道受土壤挤压作用仍持续变形。
(3)并行间距大于等于8m时,管道不再发生破裂,其变形应力来自土壤粘弹性变形应力。最大变形位置为管道正面靠近顶部位置。虽然该变形量不会导致管道破裂,但已超出管道椭圆化设计准则。
终上所述,相比于地上管道,埋地管道虽然发生爆炸的概率较低,但其爆炸冲击将引起并行管线发生大形变甚至破裂失效。为保证埋地并行管线的稳定运行,其敷设间距必须大于8m。如果敷设环境特殊,如并行间距小于6m,必须在两个管道之间设置防护板,隔离两管道间的土壤变形。
参考文献:
[1] Petrochina construction CDP-G-OGP-PL-001-2010-1, the specification of design on pipeline parallel laying, petrochina gas and pipeline company. 2010 (中国石油工程CDP-G-OGP-PL-001-2010-1 油气管道并行敷设设计规定)
[2] Dai yibin etc, The analysis of reasonable diatance on parallel oil and gas pipeline, China special equipment safety 2010 (26) 01 (代以斌等 长输油气管道并行敷设合理距离分析 中国特种设备安全 26(1))
[3] Yanbao Guo, Lugui He, Deguo Wang, Shuhai Liu Numerical investigation of surface conduit parallel gas pipeline explosive based on the TNT equivalent weight method Journal of Loss Prevention in the Process Industries, 2016
[4] Edmilson P. Silva, Marcio Nele, Paulo F.Frutuoso e Melo, László Könözsy ,Underground parallel pipelines domino effect: An analysis based on pipeline crater models and historical accidents, Journal of Loss Prevention in the Process Industries, 2016.05
[5] T.D. O’Rourke, J.K. Jung, C. Argyrou, Underground pipeline response to earthquake-induced ground deformation, Soil Dynamics and Earthquake Engineering, 2016
[6] J. Serrano-Arellano, J.M. Riesco-ávila, J.M. Belman-Flores, K. Aguilar-Castro, E.V. Macías-Melo Numerical study of the effect of buoyancy on conjugate heat transfer in simultaneous turbulent flow in parallel pipelines International Journal of Heat and Mass Transfer, 2016
[7] Leige Xu, Mian Lin Analysis of buried pipelines subjected to reverse fault motion using the vector form intrinsic finite element method Soil Dynamics and Earthquake Engineering, 2017, Vol.93
[8] J. L. C. Diniz, R. D. Vieira, J. T. Castro, A. C. Benjamin, J. L. F. Freire Stress and Strain Analysis of Pipelines with Localized Metal Loss Experimental Mechanics, 2006, Vol.46 (6), pp.765-775
[9] Changzheng Sun, Bo Yu, Yi Wang Analyses on Heating Energy Saving of Two Hot Waxy-Crude Oil Pipelines Laid Parallel in One Ditch Advances in Mechanical Engineering, 2013, Vol.2013
[10] Dong shaohua Pipeline Integrity Assessment Theory and Appliacation, Oil Industry Publisher, BeiJing 2014.6 P179-180
[11] WANG De-guo Safe distance of overhead parallel pipeline calculated by numerical simulation of gas pipeline explosion Journal of China University of Petroleum VoL. 37 No.5, 0ct.2013
[12] Zhang Zhihong,Li Kefu,Zhang Wenwei,Zhang Liming,Geng Xiaomei Boundary conditions for temperature field simulation of buried parallel pipelines 2013 v(32)6 P601-605
[13] XU Yan-xin,MA Xuehai,PANG Baohua,et a1.Nature gas pipeline security laying distance with parallel oil pipeline[J].Oil&Gas Storage and Transportation, 2011,30(11):816-818.
[14] Xiang bo, Research on the diatance of parallel pipeline and prention methods, Natural gas and oil, V0L. 27, No.3 , Jun.2009
[15] Zhang Ping,Li Kefu etc, Risk analysis for instaⅡation of parllel oil&gas pipelines Oil&Gas Storage and Transportation, 2013,32(9):1027-1028.
[16] Zhu hai , Separation Distance and Construction Technology of Parallel Laid Pipelines in the Forest Regions and Permafrost Regions , Oil-Gasfield Surface Engineering 2016.(35) 01, p83-pp85
[17] wang meng, Li qian etc, the reasonable distance analysis of oil and gas parallel pipelne, Oil and chemical euipments, 2015 V(18)11 pp62-65
上篇:
下篇:




 甘公网安备 62010202003034号
甘公网安备 62010202003034号 
