董绍华  张河苇

中国石油大学（北京）

摘要：本文从管道完整性评价的国内外研究进展出发，基于天然气管道中硫化氢的浓度和内外部载荷应力共同作用的环境影响，分析了含硫化氢管道氢致开裂影响下，建立了管道完整性评定方法，建立管道应力、材料、环境共同作用下的氢致开裂临界扩展模型，得出了氢致开裂管道的失效评定关系，重构了失效评定图，并给出了在一定输送压力和H₂S含量下，含裂纹缺陷X60和X65钢制管道的安全度和安全范围，以及含H₂S管道的极限承压载荷。对管道的安全运行具有重要指导意义。

主题词： 硫化氢   管道  缺陷  完整性评价

1．引言

断裂力学的发展，为含缺陷管道和压力容器的失效完整性提供了科学依据，1971年美国完善了ASME锅炉压力容器缺陷评定标准，至80年代末，英国焊接协会、国际焊接协会、日本焊接协会、美国机械工程师协会等相继公布了10部压力容器缺陷评定规范或指导性文件^[1~3]，这些标准按其理论分为四类：第一、以美国ASME规范为代表的线弹性断裂理论评定方法；第二、以英国BSIPD6493（1980）为代表的COD理论的评定方法；第三、以英国中央电力局（CEGB）的R6失效评定图技术；第四、以美国电力研究院的EPRI方法为代表的J积分理论为基础的评定方法。

弹塑性断裂分析中的J积分评定法^[4-6]随着计算机的发展和计算手段的完善，各种基本的含缺陷结构的J积分已经都能计算．加之美国EPRI提出的弹塑性断裂分析的工程方法，并提供了各种含缺陷结构J积分全塑性解的韧性断裂手册，解决了J积分的工程计算问题。弹塑性断裂理论研究所取得的重要进展，促使管道、压力容器缺陷评定技术又有了新的进展、这一进展的代表就是英国CEGB的R6失效评定技术的发展，英国在1986年又对R6作了第三次修订，将R6失效评定曲线的物理意义阐述得非常清楚，定义了失效评定曲线，当被评定点落在评定曲线上时，表示结构失效，若被评定点落在曲线下方，则说明结构完好。R6方法的十年发展，集中反映了近十年来弹塑性断裂理论的发展，它取K因子理论、COD理论及J积分理论等长处，以及加入其最新研究成果，使R6方法建立了科学的理论基础，进而使其成为目前国际上水平最高的压力容器缺陷评定标准，目前世界各国的压力容器缺陷评定标准均在向R6方法靠拢，相继采用失效评定图技术^[7-9]。

    但是，对于输气管道来讲，环境断裂^[10-13]是影响管道操作运行的重要因素，由于输气中H₂S的存在，在管道内部形成应力、环境、材料，此时，氢致开裂应力强度因子小于非氢条件下的临界应力强度因子，并且管道中H₂S初始浓度不同，氢致开裂应力强度因子亦不同。因此，环境断裂的安全评定问题不仅与材料的机械性能有关，而且与氢浓度的含量有关，从失效评定图上应反映氢浓度的影响和应力作用的影响。

本文考虑氢浓度和应力共同作用的影响，建立新的正确可靠的含氢致裂纹管道的完整性评定方法，并从失效评定图上反映氢浓度和应力作用的影响。考虑氢致开裂断裂判据，氢浓度对管道断裂的影响，建立了管道新的失效评定关系，并给出失效评定图。确定一定输送压力和H₂S含量下，含裂纹缺陷管道的安全度和安全范围，并给出了相应的安全系数。

2．管道缺陷裂纹的失效评定关系

J积分弹塑性的方法是管道弹塑性断裂力学的基础^[14]，这种方法是将弹性解和全塑性解相加到一起得到的弹塑性解，通过计算J积分的计算，确定出管道缺陷裂纹断裂强度因子与载荷的关系，其表达式：

                                                  （1）

其中，为按等效裂纹深度协调后的J积分弹性分量，为J积分塑性分量。

根据式（1）可推导出的管道以积分理论为基础的结构失效评定曲线方程，管道裂纹的评定关系^[15]可写为：          

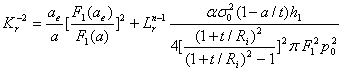                     (2)

                          

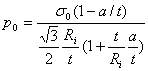
其中：为完全塑性状态（）下管材的塑性失稳压力，；、为失效点纵坐标和横坐标；,为弹塑性区修正系数； 为硬化系数；为屈服应力；为壁厚；为内径；为外径；为缺陷深度；为硬化指数；为与、以及硬化指数有关的无量纲函数。

3．含氢致裂纹管道的完整性（失效）评定曲线

氢环境下，在氢与外力的共同作用下，引起对材料的应力腐蚀作用，使材料的断裂韧性下降^[16-18]，即氢致开裂应力强度因子小于非氢条件下的临界应力强度因子，由于管道中H₂S初始浓度不同，作用的程度不同，氢致开裂应力强度因子亦不同，建立管道应力、材料、环境共同作用下的氢致开裂临界扩位错模型，如图1所示，从内聚力模型推导出临界强度

因子与氢浓度及相关参数的表达式为：

 

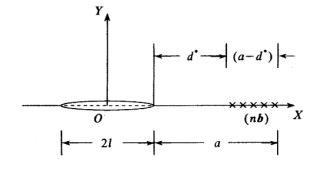
图1  氢致裂纹扩展过程区位错分布

                       

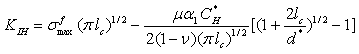                       （3）

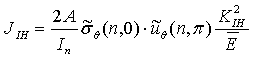                                     （4）

其中，为材料最大内聚力，为泊松比，为临界断裂长度（与管道环境无关的断裂长度，按照API579 计算得出），为裂尖至位错区距离，为具有量纲的常数，对于低碳钢来讲^[20-22]，一般可取，，为氢富集浓度， 为屈服应力，为弹性模量，为氢环境下临界积分，为氢致开裂断裂强度因子，为积分系数，为与有关的常数，、为与和有关的无量纲函数，

由于氢环境下管道材料的临界断裂应力强度因子，所以管道的承压能力下降，无氢条件下，管道的塑性极限失稳载荷为：

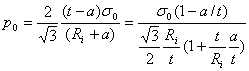                                      （5）

有氢条件下，含氢管道的极限载荷为：

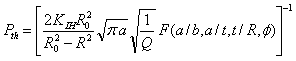                                （6）其中，为形状函数因子，，，为边界修正因子。

    在氢环境下，对于壁厚为管道来讲，裂纹深度一定时，随着载荷的增加，可能发生断裂失效，也可能发生塑性失稳失效，含氢断裂极限载荷与失稳极限载荷的关系有两种可能，一种是，另一种是。当时，认为在管道起裂之前，发生塑性失稳，令，对于管道有限长椭圆形裂纹，则含氢致裂纹管道的完整性评价评价曲线方程为：

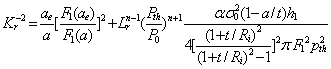                           （7）

    待评定点的坐标与的大小也与管道的操作温度有关^[19]，不同的操作温度，评价点的坐标也不同，针对氢致开裂的断裂形式，具体的参数如下：

（1） 当操作温度在下转变温度时，将出现脆性断裂，因此以作为材料的断裂韧性，评定点计算如下：

                                                 （8）

（2） 当操作温度在过渡区温度时，以作为裂纹启裂的断裂韧性，评定点计算如下：

                                         （9）

                                                               （10）

4． 含H₂S天然气管道完整性评价算例

天然气埋地输送管道，材料分别为X60和X65号钢，输送介质中湿H₂S含量为100mg/m³，管径为914mm，壁厚为14.3mm，直管轴向裂纹长度为40mm，深度为5mm，管道输送压力为8.5Mpa，管道出站输送压力为8.0Mpa，安装环境温度为20，运行介质温度为10，埋地沟深为2.2m，埋地沟宽1.5m，管线的热膨胀系数为1.2，沉陷系数为0.2，回填土密度为1800Kg/m³，管道与土壤摩擦系数为0.5，回填土内摩擦参数为0.13，沉陷量为 5mm，X60材料的弹性模量为2.0N/mm²，泊松比为0.2，临界断裂应力强度因子为为119.73MPa，硬化系数为2.235，硬化指数为6.575，屈服应力415Mpa，断裂应力为550Mpa。X65钢材料的弹性模量为2.0N/mm²，泊松比为0.20，临界断裂应力强度因子为为128.91MPa，硬化系数为2.409，硬化指数为6.695，屈服应力450 Mpa，断裂应力为585Mpa。

    对含H₂S输气管道进行完整性评价，给出管道的安全系数，并进行安全性判断。X60和X65钢埋地管道的完整性评价曲线如图1、图2所示

         图2   X60管道完整性评价曲线         图3   X65钢管道完整性评价曲线                     

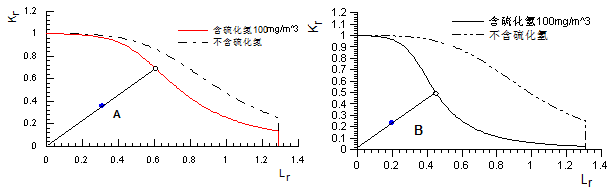
图2为X60管道完整性评价曲线，缺陷评价点A的坐标为（0.3205，0.3763），对应的安全系数为1.7367，从图中可看出，含硫化氢管道评价曲线安全区域范围变小。图3为X65钢管道完整性评价曲线，缺陷评价点A的坐标为（0.2038，0.2650），对应的安全系数为1.8375，从图中也可看出，含硫化氢管道评价曲线安全区域范围变小。

5. 结论

（1）本文首次提出了适合于氢环境下管道弹塑性断裂分析的完整性评价方法。

（2）建立管道应力、材料、环境共同作用下的氢致开裂临界扩展模型，确定了氢环境下含裂纹管道极限承压能力P和临界J积分J_IH。对氢环境下含缺陷的输气管道的安全性进行了评价，给出失效评定图和安全系数。

（3）考虑管道的埋地参数、内压、土压和摩阻力和温度的影响，应使用当量内压作为管道的评价载荷，模拟工况与现场实际吻合。

（4）氢环境与非氢环境下管道缺陷裂纹的评价安全系数比较可知，氢环境下的管道安全系数减小，并且随着H₂S浓度越大，则安全系数递减。

（5）含氢管道的安全评价系数，不仅与管道内H₂S浓度有关，而且与材料的机械性能有关，裂纹缺陷的几何形状、硬化系数、硬化指数是影响安全系数的重要因素。 因此降低输送管道中H₂S的浓度，适当提高材料的硬化系数，可增加含氢缺陷管道的安全系数。

 

参考文献

[1] PD6493, B. S. I. (1991). Guidance on methods for assessing the acceptability of flaws in fusion welded structures. British Standards Institution.

[2] Milne, I., Ainsworth, R. A., Dowling, A. R., & Stewart, A. T. (1988). Assessment of the integrity of structures containing defects. International Journal of Pressure Vessels and Piping, 32(1-4), 3-104.

[3] Anderson, T. L., Merrick, R. D., Yukawa, S., Bray, D. E., Kaley, L., & Van Scyoc, K. (1993). Fitness-For-Service Evaluation Procedures For Operating Pressure Vessels, Tanks, And Piping In Refinery And Chemical Service. FS-26, Consultants’ Report, MPC Program On Fitness-For-Service, Draft, 5. 

[4] Shlyannikov, V. N., Boychenko, N. V., Tumanov, A. V., & Fernández-Canteli, A. (2014). The elastic and plastic constraint parameters for three-dimensional problems. Engineering Fracture Mechanics, 127, 83-96.

[5] Simpson, R., & Trevelyan, J. (2011). Evaluation of J 1 and J 2 integrals for curved cracks using an enriched boundary element method. Engineering Fracture Mechanics, 78(4), 623-637.

[6] Zheng, T., Zhu, Z., Wang, B., & Zeng, L. (2014). Stress intensity factor for an infinite plane containing three collinear cracks under compression. ZAMM‐Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 94(10), 853-861. 

[7] Bloom, J. M. M. (1991). ik S N. 含缺陷压力容器及管道的完整性评定规程.

[8] Gordon, J. R., Wang, Y. Y., & Michaleris, P. (1995). Applying fitness-for-service concepts to welded structures: Special considerations for welded joints (No. CONF-950740--). American Society of Mechanical Engineers, New York, NY (United States). 

[9] American National Standards Institute. (1991). Manual for Determining the Remaining Strength of Corroded Pipelines: A Supplement to ASME B31 Code for Pressure Piping. American Society of Mechanical Engineers.

[10] Morana, R., & Nice, P. I. (2009, January). Corrosion assessment of high strength carbon steel grades P-110, Q-125, 140 and 150 for H2S containing producing well environments. In CORROSION 2009. NACE International. 

[11] Cernocky, E. P., Aaron, V. D., Paslay, P. R., & Wink, R. E. (2005, January). Combined axial tension/compression and internal pressure testing of mini-pipe specimens in H2S environment to determine three dimensional (triaxial) stress states which produce crack initiation failure: explanation of the new test fixture, mini-pipe specimen, and preliminary test results. In SPE High Pressure/High Temperature Sour Well Design Applied Technology Workshop. Society of Petroleum Engineers.

[12] Zheng, S. Q., Chen, L. Q., & Chen, C. F. (2013). Failure analysis of an A333Gr6 pipeline after exposure to a hydrogen sulfide environment. Engineering Failure Analysis, 35, 516-523.

[13] Plennevaux, C., Kittel, J., Frégonese, M., Normand, B., Ropital, F., Grosjean, F., & Cassagne, T. (2013). Contribution of CO 2 on hydrogen evolution and hydrogen permeation in low alloy steels exposed to H 2 S environment. Electrochemistry Communications, 26, 17-20. 

[14] Defect Assessment of Pressure Vessels Standard Compilation Group. (1985) Defect assessment of pressure vessels standard CVDA-1984. Journal of Mechanical Strength,1985,2 (1):1-24.

[15] Wang, H. T., Wang, G. Z., Xuan, F. Z., & Tu, S. T. (2013). Fracture mechanism of a dissimilar metal welded joint in nuclear power plant. Engineering Failure Analysis, 28, 134-148.

[16] 董绍华. (2000). 油气管道氢损伤失效行为研究进展. 油气储运, 19(4), 1-6.

[17] Knyazeva, M., & Pohl, M. (2013). Duplex steels: Part I: genesis, formation, structure. Metallography, Microstructure, and Analysis, 2(2), 113-121.

[18] Yeh, T. K., Huang, G. R., Wang, M. Y., & Tsai, C. H. (2013). Stress corrosion cracking in dissimilar metal welds with 304L stainless steel and Alloy 82 in high temperature water. Progress in Nuclear Energy, 63, 7-11. 

[19] Kim, W. K., Koh, S. U., Yang, B. Y., & Kim, K. Y. (2008). Effect of environmental and metallurgical factors on hydrogen induced cracking of HSLA steels. Corrosion Science, 50(12), 3336-3342.

[20] Ding Hongzhi，Xing Xiusan，Zhu Hesun，A  model for hydrogen induced embrittling process zone cracking with application to the Calculation of threshold stress intensity  Journal of Beijing Institute of  Technology  15(1) 1995  P55~59

[21] oriani R A, Josephic P H, Hydrogen assisted Cracking of Steel Acta Metall, 1977,25 977-985

[22] Ahhurst K N, Baker T J, the threshold stress intensity for hydrogen induced crack growth Metall Trans , 1981, 12A .P1059-1070