王新  张华兵

中国石油管道科技研究中心/中国石油天然气集团公司油气管道输送国家工程实验室 

摘要：《油气管道完整性管理规范》给出了输气管道的潜在影响半径计算公式，该公式对计算过程进行了大量简化和假设，得出了基于管道管径与压力的简化公式，在输气管道高后果区识别中得到广泛应用。通过对该简化公式存在的问题进行分析，表明简化公式在泄漏衰减因子、泄漏系数、热辐射计算模型、火灾热辐射阈值等方面的取值，都会导致计算结果与真实事故影响半径的偏差。并通过与油气管道失效后果定量评价软件RiskInsight进行实例对比分析，结果表明：简化公式计算的潜在影响半径结果偏小，管道管理者仍可以采用该公式进行快速计算，但需要注意该公式的前提假设。当需要更加严谨的计算结果时，应该采用专业软件。

关键词：输气管道；喷射火；潜在影响半径；简化公式；RiskInsight 

输气管道一旦泄漏发生火灾爆炸，将严重威胁周边人员的人身安全。输气管道事故对周边人员的影响范围，即输气管道潜在影响半径的计算一直是重要的技术问题，在GB 32167-2015《油气管道完整性管理规范》中，给出了基于管径与压力的输气管道潜在影响半径计算公式，即下文中的公式（5）。该公式最早出自加拿大C-FER 技术公司的研究报告^[1]，后来写入了ASME B31.8S标准《输气管道系统完整性管理》，国内将其采标为SY/T 6621而广为大家所知^[2]。

计算输气管道潜在影响半径需要考虑诸多因素，计算过程十分复杂，需要专业软件和专业技术人员才能完成，目前较为知名的软件有荷兰应用科学研究院（TNO）开发的Effect软件和DNV开发的SAFETI^TM软件^[3]；国内中国安全生产科学研究院开发的CASST-QRA软件^[4]；中国石油管道科技研究中心开发了油气管道失效后果定量评价软件RiskInsight，也进行了大量应用，并通过了与真实管道事故的对比验证^[5]。但为了让管道管理者快速简便进行计算，ASME B31.8S对该计算过程进行了大量简化，并做了很多假设，得到了输气管道潜在影响半径简化计算公式。本文将讨论严谨的输气管道潜在影响半径计算与该简化公式之间的差异。

1  输气管道的潜在影响半径简化公式

1.1  简化公式的主要设定

计算输气管道潜在影响半径过程中需要确定几个重要问题。

（1）泄漏速率：简化公式中泄漏速率为输气管道破裂时的泄漏速率，主要由管道管径和管道压力确定，泄漏速率采用峰值泄漏速率与泄漏衰减因子的乘积；

（2）热辐射模型：假设喷射火焰热源为一系列位于射流轴线上的点热源，采用点源模型计算火灾热辐射；

（3）热辐射阈值：采用15.8 kW/m²，计算结果为喷射火造成1%概率死亡的潜在影响半径。

1.2  计算气体泄漏速率

输气管道在发生破裂时，由于管道内压力的不断降低，天然气的泄漏速率随时间不断减小。在计算喷射火热辐射影响时，ASME B31.8S采用管道泄漏过程中的当量泄漏速率来表征泄漏速率，当量泄漏速率为峰值泄漏速率乘以泄漏速率衰减因子^[3]：

                           （1）

                                                     （2）

式中，当量泄漏速率，kg/s；释放衰减因子；为峰值泄漏速率，kg/s；泄漏系数；管道直径，m；管道运行压力，Pa；流动因子；气体声速，；气体比热比，对于甲烷取1.306；为理想气体常数J/(kg·mol)/K；为气体温度，K；为气体摩尔质量。

1.3  喷射火热辐射模型

ASME B31.8S在计算喷射火热辐射时采用点源模型，点源模型假设火焰热源为一系列位于射流轴线上的点热源，并保守认为总热辐射通量为每个点热源热辐射通量之和^[6]：

                                 （3）

式中，为热辐射通量，kW/m²；为燃烧系数，对于喷射火取0.35；X_g为辐射系数，取0.2；Q为气体泄漏质量流率，kg/s；H_c为燃烧热，对于甲烷取50 000 kJ/kg

1.4  热辐射阈值

ASME B31.8S中潜在影响半径为人员在喷射火热辐射影响下1%概率死亡的半径，所取的热辐射阈值为15.8  kW/m^2 [7]，代入式（3）可得：

                                          （4）

代入各项参数，可得潜在影响半径为：

                               （5）

公式（5）即为目前广泛使用的简化公式（以下皆称简化公式）。

2  简化公式的几个问题

2.1  泄漏衰减因子的取值

输气管道在发生破裂后，管道内压力不断降低，天然气的泄漏速率随时间不断减小，泄漏速率变化趋势如图1所示。

 

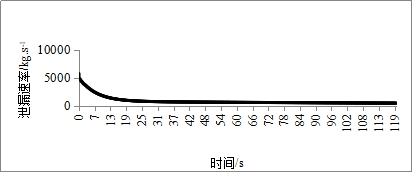
图1 管径710 mm压力8 MPa的天然气管道破裂后泄漏速率变化趋势

如图1所示，管道泄漏后泄漏速率是随时间不断变化的，在计算喷射火热辐射影响时，简化公式采用管道泄漏过程中的当量泄漏速率来表征泄漏速率。从式3可以看出，潜在影响半径与当量泄漏速率密切相关，而当量泄漏速率很大程度上取决于泄漏速率衰减因子（公式1），因此泄漏衰减因子的取值对潜在影响半径计算结果的准确性有着极大影响。荷兰应用科学研究院（TNO）对输气管道泄漏速率衰减规律进行了一系列实验研究，认为不同管道的泄漏速率衰减因子在0.20-0.50之间^[8]。英国HSE将管道泄漏衰减因子取为0.25^[9]，而简化公式在计算潜在影响半径时，将泄漏速率衰减因子保守取为0.33^[3]。即简化公式认为峰值泄漏速率降到三分之一时，泄漏速率趋于稳定。然而泄漏速率衰减因子的取值与泄漏点位置、管道直径、管道泄漏点处的压力等因素密切有关^[10]，不同管道泄漏工况的泄漏衰减因子的取值应该有所区别，将泄漏衰减因子统一取值为0.33，会造成不同泄漏工况潜在影响半径计算结果的误差。

高压天然气管道在发生泄漏时往往会在很短时间之内引发喷射火，人员对于火灾热辐射的反应时间也往往小于30 s^[11]，因此喷射火热辐射危害往往发生在发生喷射火的初始阶段，喷射火的热辐射危害与管道初始泄漏速率和质量密切相关。为了更准确的计算喷射火热辐射危害，RiskInsight软件中关于当量泄漏速率的计算方法，采用荷兰应用科学研究院紫皮书中的方法，这种方法按照管道泄漏质量将管道泄漏过程分为5个阶段，每个阶段的泄漏质量M_eff为全部泄漏质量M_all的20%，计算喷射火采用的当量泄漏速率Q_eff为第一个泄漏阶段的平均泄漏速率，这种当量泄漏速率的计算方法要更为科学合理^[12]。图2为不同管径时简化公式计算的当量泄漏速率与RiskInsight软件计算的当量泄漏速率比较，从图中可以看出简化公式计算的当量泄漏速率要比RiskInsight软件当量泄漏速率小，这样可能导致简化公式计算结果偏小。

 

 

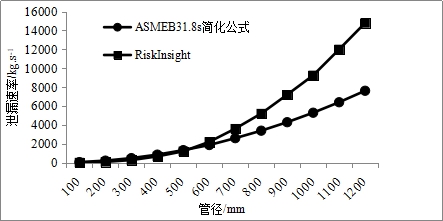
图 2  不同管径下简化公式与RiskInsight软件计算的当量泄漏速率比较

2.2   泄漏系数值的选取

天然气从管道泄漏孔口或狭缝中向外泄漏的过程中，在泄漏孔口处发生缩颈现象，即实际流动面积小于泄漏口面积，使得理论流量与实际流量有差异，因此要引入泄漏系数予以修正。泄漏系数值直接影响气体泄漏速率的计算。一般而言,泄漏系数的取值范围在0.6—1.0之间。按泄漏孔的形状可分：圆形孔值为1.00；三角孔值为0.95；长形孔值0.90^[13]。一般管道发生破裂时，泄漏系数取值为1.00，而简化公式取0.62，最终可能使得管道潜在影响半径的计算结果偏小。

2.3  热辐射计算模型的选择

目前，喷射火热辐射的数学计算模型主要有两种：点源模型和固体火焰模型（Thornton模型），简化公式选用点源模型。点源模型假设火焰热源为一系列位于射流轴线上的点热源，并保守认为总热辐射通量为每个点热源热辐射通量之和，模拟计算喷射火时过于简化火焰形状，导致计算结果准确性不高^[14]。而Thornton模型从火焰形状的角度出发，假定喷射火形状为平截头圆锥形，符合喷射火长度较长的特点，并且该模型经过风洞和场地实验验证，计算结果较为准确^[15]。图3为同样工况时固体火焰模型与点源模型热辐射计算结果对比图，从图中可以看出点源模型和Thornton模型计算结果存在差异，尤其是距离泄漏口较近时，点源模型的计算结果过大，可能导致最终简化公式的计算结果偏大。

 

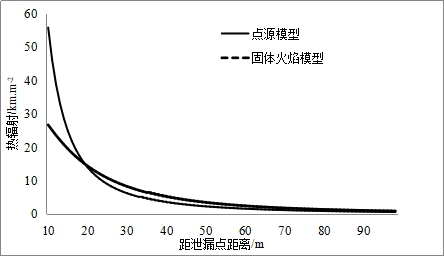
图 3  相同工况时点源模型和固体火焰模型计算结果比较

2.4  火灾热辐射阈值的选取

简化公式中潜在影响半径为人员在喷射火热辐射影响下1%概率死亡的半径，所取的热辐射阈值为15.8 kW/m²。而通常火灾热辐射的安全距离（人员基本不受影响，有轻微灼热感）计算采用的热辐射阈值为4 kW/m²，导致人员灼热死亡半径热辐射阈值为37.5 kW/m^2 [16]。因此简化公式中潜在影响半径既不是天然气管道破裂时的安全距离，也不是死亡半径，而是一个中间值。这种情况下，人员暴露会被一定程度烧伤。所以简化公式计算的管道潜在影响半径会比真正的输气管道事故人员死亡半径大，比人员基本不受影响的半径小。

2.5  爆炸冲击波影响分析

输气管道泄漏后，如果没有立即被点燃，泄漏天然气会在空气中扩散，极易与周围空气混合形成爆炸性蒸气云，如果遇到引火源将会爆炸，在输气管道泄漏后果分析中，蒸气云爆炸冲击波的潜在影响半径较喷射火要大^[17]，但由于蒸气云爆炸需要在特定的气象及地形条件下形成，其发生概率较喷射火要小，因此一般计算输气管道潜在影响半径时，很少考虑蒸气云爆炸的影响。目前应用较多的蒸气云爆炸潜在影响半径预测模型包括TNT当量模型、TNO多能法、Baker-Strehlow模型等^[18-20]，但以上模型所需参数较多，计算过程较为复杂，目前并没有简化模型来计算蒸气云爆炸潜在影响半径，只能依赖专业软件完成计算。ASME B31.8S中的简化公式也只针对喷射火计算潜在影响半径，并没有考虑蒸气云爆炸冲击波的影响。

3  实例对比分析

应用油气管道失效后果定量评价软件RiskInsight对某输气管道破裂后发生喷射火及蒸气云爆炸的影响半径进行计算，并与ASME B31.8S简化公式计算结果进行对比（见表 1、2）。

该管道管径为1 016 mm，运行压力为8 MPa，壁厚为12 mm，本次模拟泄漏点距离上游阀室9.1 km，距离下游阀室6.7 km，模拟管段长度约为17.35 km。选取风速2.6 m/s，大气稳定度D，作为气象条件计算参数，模拟工况为管道发生破裂时的火灾爆炸潜在影响半径。

 

表1  管道破裂时火灾热辐射潜在影响半径

 

表 2   管道破裂时蒸气云爆炸冲击波潜在影响半径

 

对比结果显示：ASME B31.8S简化公式只能计算输气管道发生破裂时人员1%概率死亡的潜在影响半径，且其计算结果较RiskInsight软件小。同时通过RiskInsight软件对管道破裂后的蒸气云爆炸冲击波潜在影响半径进行计算，发现蒸气云爆炸冲击波的潜在影响半径要比喷射火热辐射大。所以在确定输气管道安全距离时，还需要根据周边气象及地形条件，一旦有可能形成蒸气云爆炸，需要考虑其可能对周边人员的影响。

4  结论

综合上述分析，GB 32167-2015《油气管道完整性管理规范》中给出的输气管道潜在影响半径的计算公式是进行了大量简化的，在泄漏衰减因子、泄漏系数、热辐射计算模型、火灾热辐射阈值等方面的取值，都会导致与真实事故影响半径的偏差。管道管理者仍可以采用该公式进行快速的计算管道潜在影响半径，但需要注意该公式的前提假设，计算结果只能作为初步的估算结果，并保守使用。

参考文献：

[1]STEPHENS M J，LEEWIK，MOOREDK. A model for sizing high consequence areas associated with natural gas pipelines[C]. Alberta：The 4^thInternational Pipelines Conference，2002：759-767.

[2] American Society of Mechanical Engineers. Managing System Integrity of Gas Pipelines: ASME B31.8S-2012 [S]. New York：ASME B 31Committee，2012.

[3] 中国石油化工股份有限公司青岛安全工程研究院．石化装置定量风险评估指南[M]．北京：中国石化出版社，2007：56-98．

 [4] 贾伟，朱建新，高增梁，等. 区域定量风险评价方法及其在化工园区中的运用[J]. 中国安全科学学报，2009，19（5）：140-146.

[5] 王新，张华兵. 油气管道失效后果定量评价软件研发[J]. 煤气与热力，2017.

[6] 谷志宇，董绍华，牛景弘，等．天然气管道泄漏后果影响区域的计算[J]．油气储运，2013，32（1）：

[7]Bilo M, Kinsman P R. Thermal radiation criteria used in pipeline riskassessment[J]. Pipes & pipelines international，1997， 42（6）：17-25.

[8] TNO. Safety study on the transportationof natural gas and LPG byUnderground Pipeline in the Netherlands [R]. Netherlands organization for Applied Scientific Reserch，1982.

[9] Hill R T，Catmur J R. Risks from hazardous pipelines in the United Kingdom[R]. HSE CONTRACT RESEARCH REPORT，1994.

[10]Dong Y H，Gao H L，Zhou J E. Mathematical modeling of gas release through holes in pipelines[J]. Chemical Engineering Journal，2003（92）：237–241.

[11]何沫，廖柯熹. 输气管道潜在影响区模型关键参数取值讨论[J]. 当代化工，2015，44（3）：608-611.

[12] AdvisoryCouncilon Dangerous Substances.Guidelines for quantitativeriskassessment(Purple Book)[M].The Netherlands，2005.

[13] 霍春勇，董玉华，余大涛，等. 长输管线气体泄漏率的计算方法研究[J]. 石油学报，2004，25(1)：101-105.

[14] 刘俊娥. 城市燃气管道喷射火事故后果分析[J].河北工程大学学报：自然科学版，2007，24（4）：53-56.

[15] 王兆芹，冯文兴，程五一. 高压输气管道喷射火几何尺寸和危险半径的研究[J].安全与环境工程，2009，16（5）：108-110.

[16] American  Petroleum  Institute. Risk based Inspection Technology：API 581-2008[S]. Washington：American Petroleum Institute，2008．

[17] 王小完，马骥，骆正山．基于天然气管线泄漏蒸汽云爆炸危害分析[J]．灾害学，2013，28（3）：16-19．

[18] 张网，吕东，王婕. 蒸气云爆炸后果预测模型的比较研究[J]. 工业安全与环保，2010，36（4）：48-52.

[19] Center for Chemical Process Safety. Guidelines for ConsequenceAnalysis of ChemicalReleases [M]. American Institute of Chemical Engineers，New York：1999.

[20] 张华兵．基于失效库的在役天然气长输管道定量风险评价技术研究[D]．北京：中国地质大学，2013：53-62．

 

作者：王新， 1984年生，毕业于中国科学技术大学安全工程及技术专业，硕士，工程师，目前在中国石油管道科技研究中心从事管道风险评价相关工作。

 

《管道保护》2017年第5期（总第36期）