王良军

广东大鹏液化天然气有限公司

高铁的高架轨道在轨道不平顺、车轮不圆度及车辆轴重等影响下产生的车辆-轨道-桥梁动力相互作用会引起结构振动，并通过桥墩基础与周围土层相互作用进一步诱发附近土体、地下管道二次振动及噪声。随着轨道交通密度不断增加、载荷不断增大，由此产生的环境振动问题愈加突出，有必要对管道进行振动监测。

目前对高铁桥墩振动影响埋地管道本体的监测研究较少。评价此类周边振动或地震波对管道产生的影响均基于震速指标、土壤沉降及位移控制指标进行。这三个指标均是基于管道周边环境的变化而间接设置的，不能直接反映周边振动时管道本体受到的影响。因此，现场监测仍是研究环境震动的重要手段，合理可靠的监测能够实时定量地反映出高铁通过时对管道本体的影响及其应变变化趋势，通过有效的数据分析为管道的运行维护措施提供参考依据。

1 监测方案

在条件许可的情况下，最为直接的方法是对管道进行振动加速度测量。但由于本方案要监测的管道区域地下水丰富，周边为鱼塘，管道埋深在5 m左右，开挖难度大且风险高，所以决定采用间接方法进行测量，即现场测量桥墩的振动情况，通过模拟计算来判断管道受影响程度。

振动监测点位于武广高铁B路桥墩处，埋地管道从两条高铁轨道的高架桥下斜穿而过，如图1所示。将武广高铁B路三个桥墩编号为1、2、3，考虑到监测位置应该与管道最近，因此选择1号桥墩为监测点，如图2所示。

图1管道走向与铁路走向示意图

图2武广高铁1号桥墩监测点

1.1 监测设备

桥墩振动加速度动态监测系统由三轴加速度传感器、多通道高速数据采集仪（IMC数据采集仪）、数据分析软件、蓄电池和终端电脑组成。三轴加速度传感器将管道振动引起的电容变化转变为电压信号，由IMC数据采集仪经滤波、放大、数据处理换算为加速度值，在终端电脑上用数据分析软件还原成图形和数值。

1.2 安装方式

监测装置的安装如图3所示，加速度传感器通过黏接剂将固定底座垂直黏接在桥墩上，然后通过IMC数据采集仪连接笔记本电脑，电源由蓄电池或发电机供电，如图4所示。加速度传感器选择与铁轨平行的方向为Z轴，垂直于地面的方向为Y轴，平行于地面且垂直于铁轨的方向为X轴。

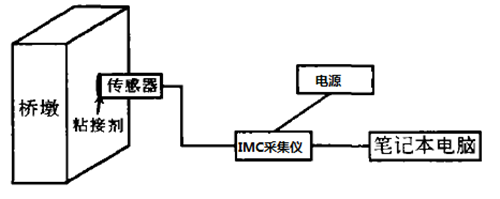
图3 监测装置示意图

图4 加速度传感器安装图

2 监测结果及分析

2.1 加速度动态监测结果

当正上方有车经过时，安装在1号桥墩的加速度传感器三轴方向都测到了明显波形，在为期7天的连续监测中，测到一组最大振动加速度值，三轴最大值分别为：X轴：0.011 g；Y轴：0.020 g；Z轴：0.009 g（监测时间：3月26日 17:09，此时段经过G71车次，列车为进站方向）。三轴的波形如图5～7所示。

图5 武广高铁1号桥墩X轴加速度波形图

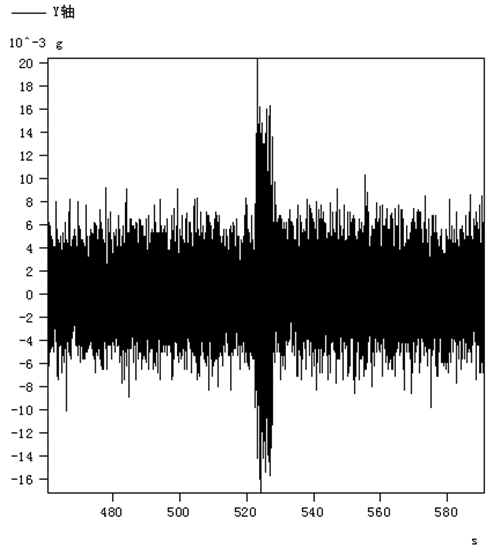
图6 武广高铁1号桥墩Y轴加速度波形图

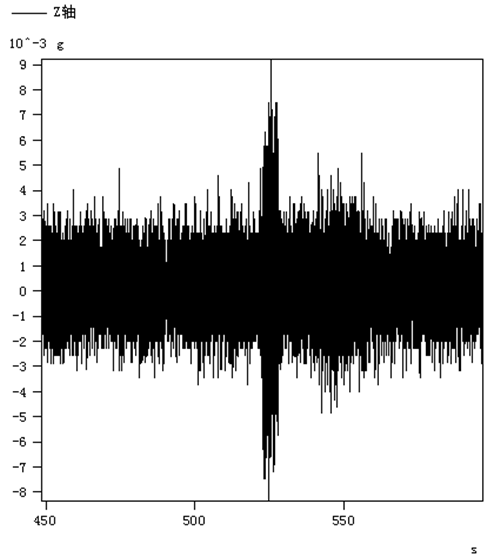
图7  武广高铁1号桥墩Z轴加速度波形图

2.2 车速与振动加速度关系分析

2.2.1 列车时速估算

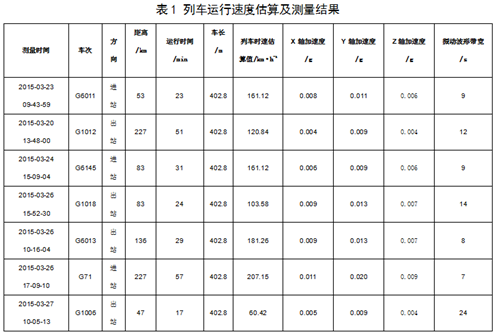
运行在武广高铁的是CRH2C型300 km/h速度等级动车，CRH2C型车是8节编组，中间车长25.0 m，两端的头车长25.7 m，列车总长度为201.4 m。两组动车头对头重联运行，共16节，总长度为402.8 m。假设以振动加速度传感器安装位置为观测点，振动测试结果峰值带宽时间就可以估算为整车通过观测点的时间t。利用公式V=s/t计算列车运行速度，结果见表1。

2.2.2 车速与振动监测结果分析

通过对表1中的列车车速、振动加速度峰值和振动带宽进行分析，发现列车经过监测位置时的运行速度越快，监测点的振动加速度峰值越高大，振动加速度波形带宽则越短，振动频率高；列车速度越慢，监测点的振动加速度峰值越低，振动波形带宽则越长，振动频率越低（见图8）。

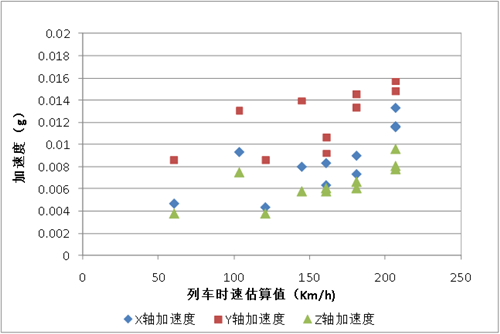
图8 列车时速与振动加速度峰值关系

2.3 数据处理方法

通过对图5~7进行分析，可以发现列车经过时，桥墩的三个方向均产生了较为明显的振动。对产生明显振动的曲线段进行FFT去噪，得到图9所示的加速度曲线。

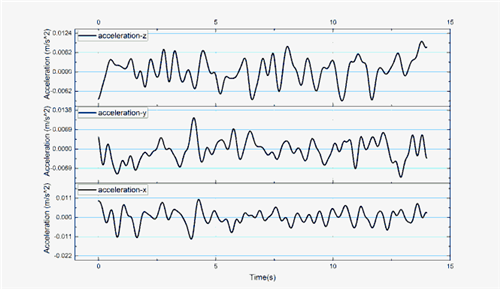
图 9武广高铁1号桥墩振动加速度曲线

图中X方向是水平方向，Y方向是竖直方向，Z方向是垂直于桥墩向外方向。对加速度曲线进行分析，可以发现三个方向的振动频率都为1.8 Hz。为了简化问题，将桥墩的振动近似看成是简谐振动，其加速度方程为：

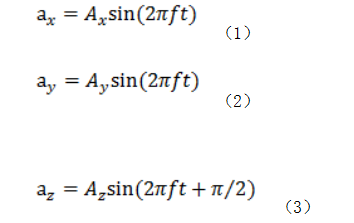
分别对加速度求积分和二次积分，可以得到速度和位移的方程如下：

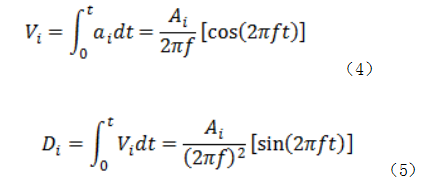
测点的速度和加速度曲线的数值积分结果如图10、11所示。通过速度变化曲线可以看到，最大峰值振动速度为0.01 mm/s。

图 10 振动速度变化曲线/mm﹒s-1

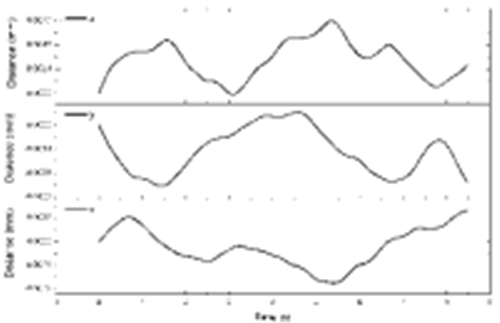
图 11振动位移变化曲线/mm

3 有限元模拟计算分析

本次计算采用的管道直径为610.0 mm，壁厚12.7 mm。由于振动对管道的影响区域主要集中在震源中心附近，因此取管道的长度为50 m，两端采用固定约束，管道外表面受到土弹簧的约束。将测量得到的加速度数据施加在模型的中心区域。为计算方便，采用壳单元S4R，模型总共划分为12040个节点和12000个单元。

3.1几何模型及网格划分

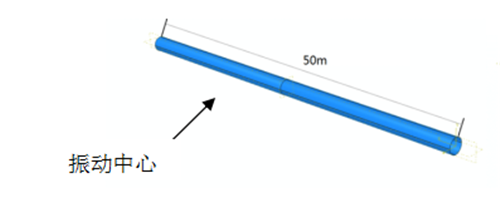
图 12 管道几何模型

图13  网格划分（12040节点，12000单元）

3.2 土壤的力学行为

与管道交互作用的土体可以等效成三个维度的弹簧。如图14所示，在管道的接点上分别连接轴向、水平和竖直方向的土弹簧，分别表示管道的轴向摩擦力、水平和竖直方向的压力。其中KA、KH、KV分别表示三个方向弹簧的刚度系数。

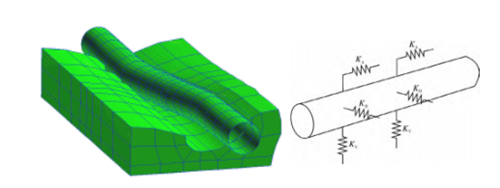
图 14  管土相互作用简化模型

土弹簧的载荷与变形特性在一定变形区间内是线性关系，超出范围的可以看成是塑性变形。另外，竖直方向的土弹簧拉伸和压缩刚度系数并不相等。计算采用如图15所示的弹簧模型。

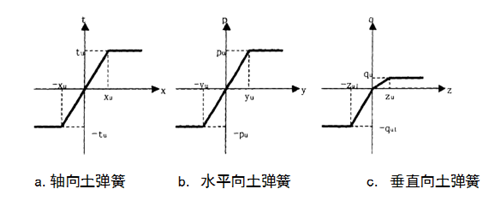
图15 弹簧模型

3.3计算结果

对管道距离桥墩最近的部位施加振动加速度的约束，本模型中对应管道的中心部位。在振动加速度驱动下求解应力场和应变场的结果。

（1）应力场

图 16  应力场/Pa（P点应力值位于波峰时刻，变形放大10000倍）

图 17  应力场/Pa（P点应力值位于波谷时刻，变形放大10000倍）

图16、17中的P点为振动中心，其振动强度最大。P点处的米塞斯等效应力场的变化曲线如图18所示。从曲线可以看到，管道振动时等效应力呈波浪状变化，最大可以达到0.5 MPa。

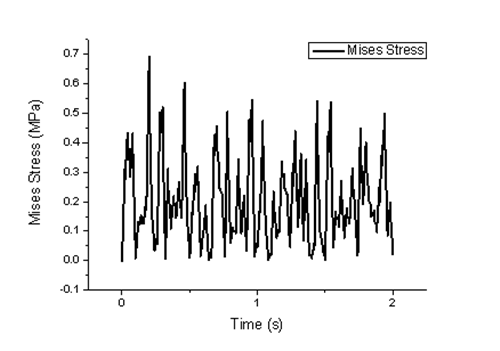
图18  震源中心P点的等效应力变化曲线/MPa

（2）应变场

图19和图20是振动状态下的应变场，最大应变值为1.6微应变，远小于地质沉降带来的变形，因此可以忽略振动所引起的变形量。

图 19  应变场（P点应变值位于波峰时刻，变形放大10000倍）

图 20  应变场（P点应变值位于波谷时刻，变形放大10000倍）

（3）计算结果

对列车通过桥墩时的管线受迫振动和两个振动的干涉情况均进行了数值仿真，计算结果表明管道的应力和应变均很小，不会对管道产生破坏性的变形。

4结论

通过现场实测，得出如下结论。

（1）本文监测点处高铁列车通过时产生的震动加速度传感器三轴方向都监测到了明显波形，最大加速度0.020 g；最大峰值振动速度为0.01 mm/s。

(2)高铁列车经过监测位置时的运行速度越快，监测点的振动加速度峰值越高，振动加速度波形带宽则越短，振动频率高。列车速度越慢，情况相反。

（3）采用有限元分析，结果表明当前工况下高铁桥墩振动时，管道的应力和应变均很小，振动对管道变形影响很小，不会对管道产生破坏性的变形，管道可以安全使用。

作者：王良军，男，1971年生，博士；主要从事与LNG 接收站、天然气长输管道及管道完整性管理相关的技术工作。

《管道保护》2017年第3期（总第34期）