张杰  张瀚  梁政

西南石油大学机电工程学院

摘 要：地面局部堆载易造成埋地油气管道出现截面椭圆化、局部破裂、防腐层脱落等，从而导致管道过早失效。为了揭示地面堆载区埋地管道失效机理，建立了管土耦合数值计算模型，对地表载荷下埋地管道的应力、应变、椭圆度等进行了研究，探讨了载荷参数、管道参数、围土参数对管道力学行为的影响规律。结果发现地表堆载作用下的无压管道比压力管道更容易发生失效；对易发生堆载段，增加管道壁厚和埋深可增强其抗变形能力；地表堆载范围和重量越大管道越易发生失效；埋地管道截面椭圆度随围土弹性模量、泊松比、黏聚力的增大而减小。

关键词：埋地管道；地面堆载；力学行为；失效分析

在管道周边施工作业中，经常出现地面堆载、超载情况，甚至出现许多违章建筑物，从而导致软土地基产生变形挤压地下管道，使其发生不均匀沉降、变形等，最后引发安全事故[1]。特别在长江三角洲和沿海地区等广泛分布有海相或湖相沉积软土，其承载能力低、孔隙比大、压缩性高、灵敏度高、易扰动[2]。因而，当地面出现堆载情况时，地表局部沉降量大，持续时间长，将对埋地管道造成极大危害。

地表堆载对管道的主要破坏形式为[3]：出现管道“盲段”，使常规的检测和维护较为困难；管道截面变形，降低了清管器的通过性，易造成管道堵塞；管道出现沉降变形，导致管道破裂、油气泄漏；易破坏管道防腐层，加速管道腐蚀。

1 堆载区管道静力分析

如图1所示，在地表载荷作用下，沟埋管道所受垂直土压力可分为两部分[4]：①由回填土自重产生的随埋深增加而增加的管顶土压力；②由地表载荷使回填土发生相对位移而施加到管道上的附加载荷，随埋深的增加而减小。

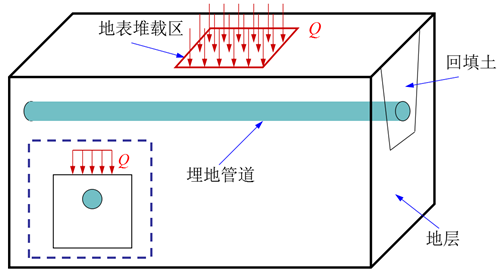
图1  地表堆载区埋地管道示意图

目前关于管顶垂直土压力的计算模型较多，如基于极限平衡理论的土柱滑动面模型和经验集中系数模型等，但二者都是基于Marston土压力模型。对于沟埋式管道，假定管沟内任一深度平面上回填土的竖向压力均匀分布，且管顶承担全部土压力，则管顶竖向土压力为：

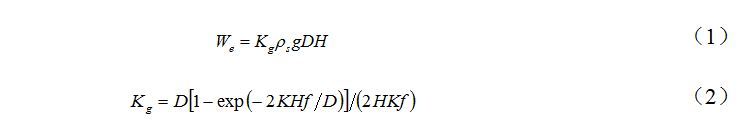
式中，We 为单位长度管顶土压力；Kg 为管顶竖向土压力集中系数；K为水平土压力系数；f 为管土摩擦因数；ρs 为围土密度；D为管道外径；H为管顶回填土厚度。

埋地管道除了承受土体自重载荷外，还将承受各种地表载荷，它们通过围土传递给管道。常用的附加载荷计算方法有Boussinesq法和扩散角法。已有研究表明，深层土体适宜采用Boussinesq法，而扩散角法仅适用于浅层土体。《输油管道工程设计规范》和《输气管道工程设计规范》都采用Spangler-Iowa方法校核外载作用下的管道截面径向变形。

Spangler-Iowa方法管道示意如图 2所示，作用于管顶的垂直载荷按均布载荷考虑，其分布宽度与管道外径相同。管底承受地基垂直反力，均匀作用于圆心角2γ，管侧承受土壤弹性抗力，其强度为二次抛物线规律分布，作用范围对应圆心角β，最大抗力qh位于水平直径的两端。

式中，Δ为管道水平径向最大变形；J为管道变形滞后系数，宜取1.5；K为管道基座系数；R为管道半径；E为管道弹性模量；I为单位长度管壁截面惯性矩；E′为地基系数。

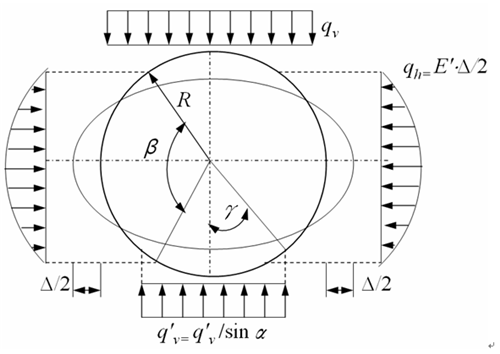
图2   Spangler-Iowa方法管道承载示意图

2  堆载区管道数值模型

如图1所示，假设地面堆载区域为矩形，载荷均匀分布。回填土厚度为1 m，地表载荷区域为1.5 m×0.8 m，埋地管道直径为660 mm，壁厚为8 mm。

以X65钢级管道为例，选用理想弹塑性Mohr-Coulomb模型来描述岩土的本构关系，地层与回填土材料相同，其弹性模量20 MPa，泊松比0.3，密度1 840 kg/m3，黏聚力15 kPa，内摩擦角15°，管土之间的摩擦系数为0.3。对模型做以下假设：载荷区内为均布载荷，并作用在管道正上方；地层和回填土均为单相材料，且各向同性，不混合其他沙粒、石块[5,6]。

3 压力管道力学行为

当地表载荷为0.5 MPa、载荷区域为0.8 m1.5 m时，不同内压管道的应力应变响应如图3所示。由内压引起的管道周向变形可以抵抗外载引起的管道变形。图3（a）表明载荷区部分管道应力随内压增加有所降低，但其余部分管道应力则随内压的增大而增大。在载荷区下方，无压管道的高应力区最大；对于压力管道，高应力区只集中在管道顶部，且高应力区面积随内压的增大呈先减小后增大趋势变化。这是由于内压较小时，地表载荷对管道的影响大于内压，随着内压的增大，它可以抵消部分地表载荷的影响，因而管道高应力区随内压的增大而减小；当管道内压较大时，内压对管道的影响非常明显，因而在内压和地表载荷的联合作用下，管道高应力区逐渐增大。根据管道中间截面应力分布可知，管道截面90°左右位置的应力较小，而管顶应力大于管底，无压管道的应力大于压力管道，且其塑性变形部位较大。因此，地表堆载作用下的无压管道比压力管道更容易发生失效。

图3（b）中，随着内压增大，管道最大等效塑性应变先减小后增大，无压管道的塑性应变最大，塑性变形区主要出现在管道顶部，管道下半部分未发生塑性变形，无压管道的两侧也发生了塑性变形。随着内压的增大，椭圆形塑性区的长半轴逐渐减小，而短半轴则逐渐增大。

图3（c）中，随着内压的增大，管道沉降量逐渐增大。由于高压管道的等效刚度较大，地表载荷能量更多地被围土吸收；而无压管道刚度较小，管道变形吸收了部分能量，因而围土吸收的能量相对较少，因而无压管道的沉降量最小。管道截面椭圆度随着内压的增大而减小，且其变化率也逐渐减小。

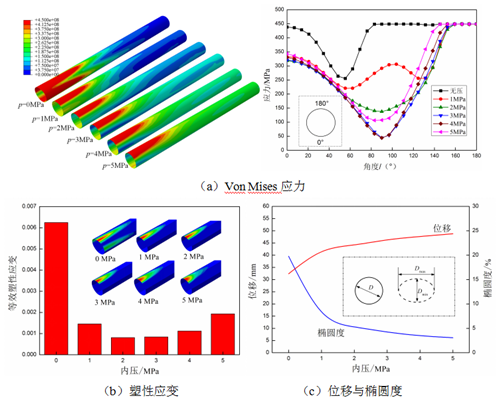
图3  不同内压埋地管道应力应变响应

4  无压管道力学行为

（1） 堆载大小

地表载荷越大，其对埋地管道产生的附加力就越大，不同载荷大小作用下埋地管道应力应变响应如图4所示。图4（a）中，当地表载荷较小时，最大应力出现在载荷区域下方管道顶部，且呈椭圆形分布。随着载荷增大，管道最大应力逐渐增大，且高应力区沿管道轴向和周向扩展。随着载荷的持续增加，高应力区仍在管道上半部分，但管道下半部分的应力也继续增大。当地表载荷小于0.4 MPa时，管道未出现塑性变形。随着载荷的增大，椭圆形的塑性变形区域出现在管顶。当地表载荷大于0.45 MPa时，管道的两边也出现了塑性区，管道最大等效塑性应变随着地表载荷的增大而增大。

图4（b）中，随着地表载荷增大，管道沉降量逐渐增大。当地表载荷小于0.2 MPa时，管道最大沉降量仅为1.3 mm。管道最危险截面椭圆度随着地表载荷的增大而增大，当地表载荷小于0.4 MPa时，管道仅发生弹性变形，且椭圆度变化率非常小。当进入非弹性阶段后，管道椭圆度较大且出现塑性变形。此时，管道承载能力急剧降低，不利于清管工作，且易出现裂纹[7]。

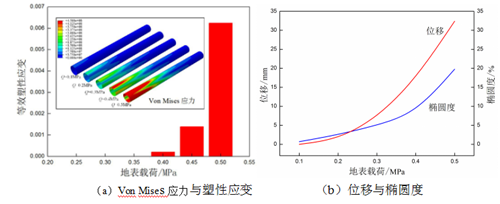
图4  不同载重下埋地管道应力应变响应

（2）管道径厚比

不同径厚比管道的应力应变响应如图5所示。图5（a）中，随着径厚比减小，管道最大应力和高应力区也逐渐减小；当径厚比为110时，管道高应力区最大，其截面发生了屈曲。当管道截面发生失稳以后，其应力分布发生了较大的变化。因而，地表堆载作用下的薄壁管道更容易发生屈曲。

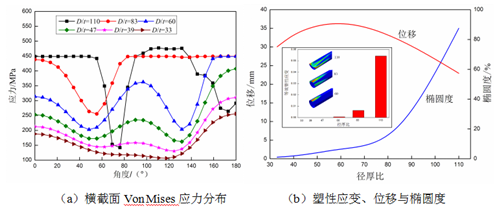
图5 不同径厚比埋地管道应力应变响应

图5（b）中，当径厚比为60时，管道未出现塑性变形。随着径厚比增大，管道的塑性应变和塑性变形区域均增大。塑性变形区最先出现在管道顶部，随着径厚比增大，管道两侧也逐渐进入塑性区。对于薄壁管道，地表堆载作用下易出现凹陷，截面呈新月形。随着径厚比增大，管道沉降量先增大后减小，管道临界径厚比为60；当径厚比小于60时，管道处于弹性变形阶段，地表堆载作用下管道弯曲应变非常小，管道沉降量随着径厚比增加而增加；当径厚比大于60时，管道进入塑性阶段，薄壁管道吸收了较多附加能量，因而，管道沉降量随着径厚比增大而减小。管道截面椭圆度随着径厚比增大而增大，且其变化率也逐渐增大。

（3）管道埋深

地表载荷对管道产生的附加力随埋深增加而减小。不同埋深下管道应力应变响应如图6所示，管道最大应力和高应力区随埋深增加而减小，同时管道下半部分的应力也逐渐减小。当管道埋深为1 m时，其上半部分截面呈现了塑性变形。因而，浅埋管道在地表堆载作用下更容易发生失效。对于人类活动较为频繁的区域，可增加管道埋深以降低其失效概率。

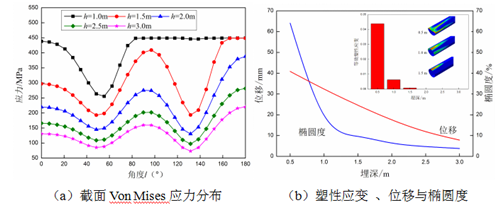
图6 不同埋深下管道应力应变响应

图6（b）所示管道最大等效塑性应变随着埋深的增加而减小。当埋深大于1.5 m时，管道未出现塑性变形；而当埋深小于0.5 m时，管道变形非常严重，出现了较大凹陷区域。管道沉降量随埋深的增加而减小，当埋深为3.0 m时，沉降量仅为7.83 mm。管道截面椭圆度也随着埋深的增加而减小，且变化率也逐渐减小。当埋深为1.5 m时，管道椭圆度为9.6%。在弹性变形阶段，管道椭圆度变化率非常小。因而，增加埋深是降低地表堆载影响的有效途径之一。

5 围土特性对管道力学行为影响

（1）围土弹性模量

围土是地表载荷与埋地管道的中间媒介，地表载荷对埋地管道产生的附加力通过围土作用在埋地管道上。因而，围土物理性质对管道应力应变有着重要影响。当地表载荷为0.5 MPa、载荷区域为0.8 m1.5 m时，不同弹性模量围土中的管道应力应变响应如图7所示。图7（a）中，管道高应力区随着围土弹性模量增大而减小，且管道下半部分的应力也随之减小。当E=10 MPa时，压载区下方的管道发生屈曲，这是由于低弹性模量围土变形较大，上覆土对管道作用力就越大所致。

图7（b）中，管道最大等效塑性应变随着围土弹性模量增加而减小。当E≥20 MPa时，管道塑性应变变化率非常小，且塑性应变分布较为接近。但当E=10 MPa时，管道却出现了较为严重塑性区，因而，在敷设管道回填时，需要严格关注回填土的选择。埋地管道的沉降量和截面椭圆度均随围土弹性模量的增加而减小，但其变化率也逐渐减小。

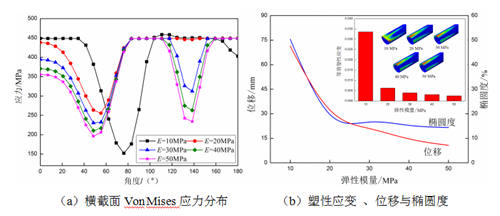
图7 不同围土弹性模量中埋地管道应力应变响应

（2）围土泊松比

不同泊松比围土中埋地管道的应力应变响应如图8所示，管道应力分布基本相同。管道高应力区随着围土泊松比的增大而减小，但变化率较小。不同泊松比围土中的管道塑性应变分布也基本相同，最大等效塑性应变均出现在管顶，但它随着围土泊松比的增大而减小，当泊松比大于0.3时，塑性应变的变化率较小。管道沉降量和截面椭圆度均随着围土泊松比的增大而减小，当泊松比大于0.3时，管道椭圆度变化较小。

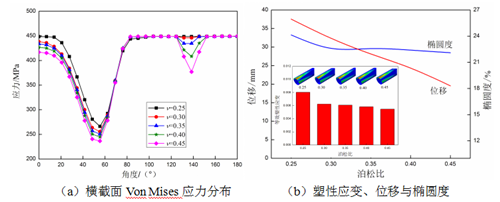
图8 不同围土泊松比下埋地管道应力应变响应

（3）围土黏聚力

黏聚力体现了相同材料中邻近部分的相互吸引力。图9所示为不同黏聚力围土中埋地管道的应力应变响应。管道最大应力和高应力区均随着围土黏聚力增大而减小。当c=10 kPa时，载荷区下方管道出现了一个较大凹陷，管道截面变为新月形，表明当管道位于砂土地层中时更容易发生失效。当c>30 kPa时，管道最大应力仅出现在管顶位置。

图9（b）中，当c>30 kPa时，管道不会出现塑性变形。管道最大等效塑性应变和塑性变形区均随围土黏聚力的增大而减小。当c=40 kPa时，管道塑性变形区非常小。管道沉降量和截面椭圆度均随围土黏聚力的增大而减小。在管道发生屈曲以前（c ≥30 kPa），管道沉降量和截面椭圆度的变化率均非常小。因而，对于有埋地管道的砂土地层、粉土地层或其他黏聚力较小土体，必须严格控制地表载荷的大小，降低埋地管道的失效几率。

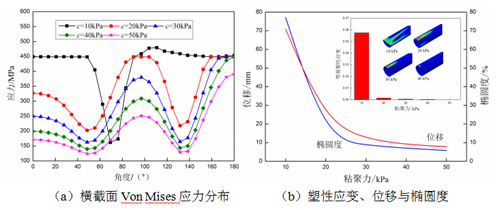
图9不同围土黏聚力下埋地管道应力应变响应

6  结论

（1）随着地表载荷的增大，高应力区沿管道轴向和周向扩展，同时管道最大等效塑性应变、沉降量、最危险截面椭圆度随着地表载荷增大而增大。因而，应该严格控制埋地管道上方大面积堆载情况的发生。

（2）随着内压增大，管道最大等效塑性应变先减小后增大，无压管道的塑性应变最大，塑性变形区主要出现在管道顶部，管道下半部分未发生塑性变形，无压管道的两侧也发生了塑性变形；随着径厚比的增大，管道的应力、塑性应变和塑性变形区域均增大，对于薄壁管道，地表堆载作用下易出现凹陷，截面呈新月形；同时，浅埋管道在地表堆载作用下更容易发生失效。

（3）管道应力、等效塑性应变、沉降量和截面椭圆度均随围土黏聚力、泊松比、弹性模量的增大而减小。

参考文献：

[1]梁政，张杰，韩传军.地质灾害下油气管道力学[M]. 北京：科学出版社，2016.

[2]孙中菊.地面堆载作用下埋地管道的力学性状分析[D].杭州：浙江大学，2014.

[3]王晓霖.典型不良地质条件下埋地管道安全评定方法研究[D].北京：中国石油大学，2009.

[4]帅健.管线力学[M]. 北京：科学出版社，2010.

[5]韩传军,张瀚,张杰. 地表载荷对硬岩区埋地管道应力应变影响分析[J].中国安全生产科学技术,2015.11(7):23-29.

[6]韩传军,张瀚,张杰.地表夯击载荷作用下埋地管道力学分析[J].中国安全生产科学技术,2015.11(10):61-67.

[7]Jie Zhang, Zheng Liang, Han Zhang. Mechanical behavior of oil and gas pipeline impacted by rockfalls [M]. LAP LAMBERT Academic Publishing, 2016.

作者：

张杰，男，1987年生，博士，讲师，硕士生导师，主要从事管道力学与安全评价、油气装备强度及服役行为研究，出版专著《地质灾害下油气管道力学》，发表相关论文40余篇。

《管道保护》2017年第6期（总第37期）