刘承磊1 李晓晖1 尤杰1 傅友1 陈彦云2 刘家辰2
1.中油管道检测技术有限责任公司油气管道输送安全国家工程实验室； 2.长庆油田分公司第十一采油厂

摘 要：传统的管道剩余寿命预测方法容易造成预测结果过于保守。通过分析内检测过程中的误差来源和分布特性，基于正态分布的统计学原理，建立了改进腐蚀生长速率计算模型，并在工程实例统计和对比分析中得到改善，有助于制定更加可靠的管道检测维修计划，具有良好的应用价值。

 

传统基于内检测数据的腐蚀生长速率计算，一般通过一次或多次管道内检测数据对比结果，通过检测时间间隔内的生长尺寸变化计算其生长速率，进一步预测管道的剩余寿命[1-3]，生长速率计算通常基于保守的原则。由于管道内检测技术存在一定的局限性，这种生长速率计算方式可能会造成评价结果过于保守。

改进腐蚀生长速率计算模型考虑了管道内检测的测量偏差和检测数据存在的离散误差。两次内检测缺陷深度服从一定均值μ和方差σ 的正态分布，最终计算出的缺陷各自的生长速率也服从正态分布。通过建立腐蚀缺陷生长速率的正态分布模型，结合DNVRP-F 101标准相关规定，选取腐蚀缺陷95%分位数对应的生长速率进行剩余寿命预测。

1 腐蚀生长速率计算

根据内检测数据对比结果，应从保守性和合理性的角度出发，结合管段自身特点、缺陷生长特性以及内检测精度指标等因素，合理计算并选取缺陷生长速率值。

1.1 传统工程使用的计算方法

基于管道内检测数据对比的腐蚀缺陷生长速率计算普遍采用线性生长模型，即认为两次内检测的时间间隔内，腐蚀缺陷呈匀速或线性增长，并且仅考虑缺陷深度的增长[4]。生长速率计算公式（1）如下。

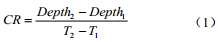
其中：CR为缺陷的生长速率；

Depth2为本次检测的缺陷深度， mm；

Depth1为上次检测的缺陷深度， mm；

T2为本次检测的日期；

T1为上次检测的日期。

由于管道运营过程中存在的各类不确定因素以及内检测的测量误差等原因，通常腐蚀生长速率计算基于保守的考虑。充分保证结果的保守性就容易造成维护维修成本的增加，给管道运营，尤其是管道服役中后期的运营带来巨大的压力。

1.2 改进的腐蚀生长速率计算模型

内检测技术在数据采集和缺陷量化过程中都会产生一定的误差。行业普遍认为，内检测的误差来源分为两类：测量偏差和数据离散。测量偏差是指重复性检测过程中同一缺陷的平均检测值与真实值之间的偏差；数据离散则反映了重复性检测过程中同一缺陷不同次检测值之间的分散程度[5]。测量偏差一般是由于内检测设备本身特性和现场运行等因素造成；而数据离散则取决于内检测精度指标。

一般认为，如果两次内检测采用相同的内检测设备和缺陷量化模型，则测量偏差可以最大程度的予以降低消除，此时内检测误差来源于数据离散，仅与内检测精度指标有关。这种情况下，缺陷的检测深度服从一定均值μ和标准差σ 的正态分布，其中均值μ等于缺陷的实际尺寸，标准差σ 可以结合内检测精度指标和正态分布特点计算得到，如图 1。

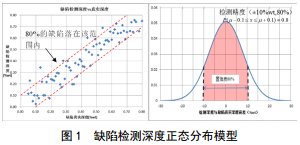
根据正态分布规律，如果两次检测的缺陷深度分别服从正态分布N1（μ1,σ12）和N2（μ2,σ22），则两次深度差值服从正态分布N3（μ2-μ1，σ12+σ22）。

根据公式（1），缺陷的腐蚀速率也可以用正态 分布模型加以描述，如图2所示。

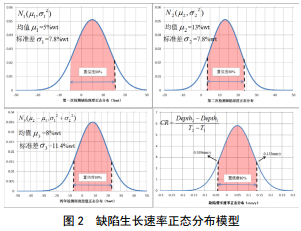
基于内检测数据对比和以上计算过程，可以确定每一缺陷的生长速率正态分布模型。 DNV-RP-F 101- 2015中2.9.2.1章节对管道剩余寿命预测进行了描述， 推荐选取95%分位数对应的生长速率值计算管道剩余 寿命，如图 3所示。其计算公式为μ+1.645σ。 该计算模型既能较为合理的反映各个缺陷的生长特性；又充分考虑了内检测的精度误差。

2 实例分析

以国外某管段A为实例，通过两次内检测数据对比，分析缺陷生长特性，分别基于传统和改进的生长速率计算模型，预测管道剩余寿命，分析和比较剩余寿命预测结果。

该管道为32英寸原油管道，于2006年建成投产，分别于2009年和2015年采用同一高清漏磁检测设备进行了漏磁检测。

2.1 两次内检测数据对比统计分析

该管段在2009年首次检测中共发现2 523处外部金属损失缺陷， 2015年次轮检测中发现了3 074处外部金属损失缺陷。通过内检测数据对比，得到两次检测深度对比和缺陷生长速率统计，如图 4所示。

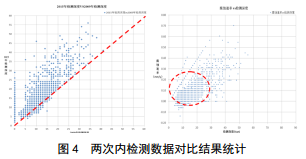
通过两次检测深度对比发现，绝大多数金属损失在检测时间间隔内出现了生长，并存在部分新增的金属损失。但大部分缺陷的生长速率较低，腐蚀速率在0～0.2 mm/y之间的缺陷2 370处，约占总数的78 %。仅部分缺陷速率较高，最高速率值达0.7 mm/y。

2.2 缺陷生长速率计算

两次内检测采用相同的检测设备和量化模型，误差取决于内检测精度指标，符合正态分布。内检测精度指标和对应标准差如表 1所示。

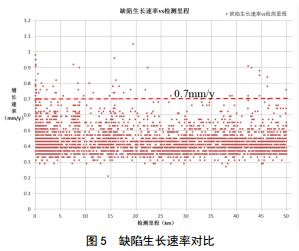
分别选取传统的最大生长速率（通过2.1确定为 0.7 mm/y，记为速率1）和改进计算模型确定的生长速率（记为速率2），预测管道缺陷剩余寿命，两种生长速率对比如图 5。

2.3 剩余寿命预测结果对比

基于两种缺陷生长速率得到管道缺陷处剩余寿命预测结果，进行统计分析和对比，基于速率1的缺陷剩余寿命绝大部分集中在9～15年（84.7%）；而基于寿命2的缺陷剩余寿命大部分大于15年（78.1%），保守程度明显下降。

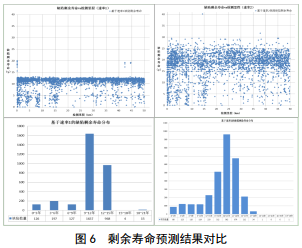
根据以往工程经验，以5年作为维护维修计划周期，对5年需要计划维修的金属损失进行统计分析，如图 6。结果显示，基于速率1计算得到的计划维修缺陷点数量（265处）多于速率2（164处）；两种速率得到的计划维修点大部分集中在检测里程的前18 km，有明显的聚集趋势，分别占总数的70.9 % （188处）和76.8 %（126处）。

从缺陷深度的角度分析，计划维修缺陷中深度30% wt以上的缺陷数量基本相同，但基于速率1得到的深度0～30% wt范围内的计划维修缺陷点数量较多；从计划维修年份角度分析， 2015年（立即维修点）和2016年计划维修的缺陷点数量基本持平，但2017至2020年，计划维修的缺陷数量差别逐年增加；基于速率1得到的计划维修缺陷点中，深度范围为0～30% wt的缺陷点数量较多且剩余寿命集中在3～5年，分析结论具有一致性。

通过剩余寿命预测结果统计分析，基于速率2的缺陷剩余寿命两种方法得到的计划维修缺陷点沿检测里程分布规律基本相同；深度30% wt以上和计划维修年在1年以内的缺陷点数量几乎没有差别；但由于速率1计算的保守性，有相当数量深度范围0～30% wt的缺陷点需要在3～5年内计划维修。因此，基于速率2的剩余寿命预测方法，在制定5年甚至更长的维护维修计划时，会得到较为合理的结果；而基于速率1的剩余寿命预测方法则可能会出现较多不必要的维修点，造成运营成本的增加。

3 结论

（1）基于两轮或多轮内检测数据对比分析流程主要包括环焊缝对齐、缺陷对齐、缺陷匹配和缺陷生长特性分析，将内检测数据集对比和信号对比相结合，保证数据对比的准确性，为腐蚀缺陷剩余寿命预测提供良好的数据基础。

（2）采用相同的检测设备和缺陷量化模型，则可以认为内检测误差仅来自数据离散，缺陷检测深度服从正态分布，以此为基础建立了腐蚀缺陷生长速率的正态分布模型。

（3）改进的管道腐蚀速率计算方法更加符合腐蚀缺陷实际的生长特性，有助于管道运营商全面深入的了解和监测管道的腐蚀生长状态，制定更加可靠的检测周期和维护维修策略，具有良好的应用价值。

参考文献：

[1]姜晓红，洪险峰，刘争，张新荣，陈敏娟. 管道内检测数据对比对完整性评价的影响[J]. 油气储运，2016， 31(1):28-31.

[2]王良军，李强，梁菁嬿 .长输管道内检测数据比对国内外现状及发展趋势 [ J ] . 油气储运， 2015,34(3):233-235.

[3]王丹丹，林晓，骆秀媛，詹燕红. 海底管道两轮漏磁内检测数据的比对方法[J]. 海船工程，2016,45(3):122-126.

[4]林现喜，张克政，陈剑健，李银喜，周信，王联伟. 油气长输管道腐蚀速率计算方法评述[J].2016.35(2):192-197.

[5]Kevin Spencer, ShahaniKariyawasam, Cathy Tetreault,Jon Wharf .A Practical Application to Calculating  Corrosion Growth Ratesby

Comparing SuccessiveILI Runs From Different ILI Vendors.[C].Calgary,Alberta, Canada: IPC Press, 2010.

作者：刘承磊， 1990年生， 2012年毕业于西南石油大学石油天然气安全工程专业， 2015年毕业于中国石油大学（北京）安全技术及工程专业，硕士，工程师，主要从事管道完整性评价相关工作。