王志月 张剑锋 屠明刚

中石油管道有限责任公司西气东输分公司

摘 要：针对天然气场站工艺管道结构复杂、高压力、流速快等特点，在应用多元统计分析算法的基础上，采用果蝇优化算法(FOA)对支持向量机(SVM)管道内腐蚀预测模型进行优化训练，建立FOA-SVM预测模型，具有建模结构简单、非线性拟合好、参数少、易调节、易于理解和实现等特点，利用125个实测数据样本对模型的预测结果进行检验，综合方差和均差为1.397×10-3、 0.0374，相比灰色模型和BP神经网络预测结果更贴近实际值，避免了BP神经网络模型预测局部最优和灰色模型误差大的缺点，为管道剩余使用寿命和剩余强度计算提供有力的数据支撑。

 

天然气长输管道是国家能源输送的生命线和动脉，具有接受天然气、给管道天然气增压、分输天然气、配气、储气调峰、发送和接受清管器等功能，是天然气输送过程中的关键环节。由于天然气集输过程中伴随CO2、 H2S、杂质等有害物质的腐蚀，以及流速对管道的冲刷腐蚀，管道腐蚀的随机性、模糊性使得腐蚀因子与腐蚀速率之间的关系呈现着复杂的非线性关系,会造成集输管线断裂、爆炸及泄漏，破坏下游用户的平稳供气，带来的危害不仅给国家造成很大的经济损失，也威胁工作人员的生命安全。现今关于预测管道内腐蚀速率的算法较多[1-6]，单一的模型已经不能满足预测精度的需求，如陈永红[5]等将灰色系统理论与马尔科夫相结合，建立灰色马尔科夫组合模型，得到了灰色无偏优化模型，使得预测数据得到了提升；胡松青[6]等建立的BP神经网络模型对输油管道内腐蚀速率预测进行预测，预测了硫含量、酸值、温度、压力、流速因素对管道内腐蚀规律的影响。本文中所述的FOA-SVM模型对天然气场站工艺管道内腐蚀速率的预测与实测数据、灰色马尔科夫组合模型、BP神经网络模型进行对比分析，结果表明FOA-SVM模型预测值更为准确，避免了BP神经网络模型预测局部最优和灰色模型误差大的缺点，确定了预测管道内腐蚀速率新方法。

1 SVM基本理论

SVM是由统计学理论而来，主要针对小样本数据进行学习、分类和预测的一种方法，“低维空间”上的点或线映射到“高维空间”，寻找一个平面将这些点或线分离，这种线形函数统称为“超平面” [7,8]。通过松弛变量和核函数（Kernel）处理实现低维到高维的转化，线性不可分转化为可分，最后对转化之后的样本进行线性分析[9-12]。

假设样本为(χ1 ,χ2 , ...χn .)∈Rn， (y1 ,y2 ,...yn .)∈R， χ∈RN 为输入参数， y∈R为相应的输出参数， n为样本个数。 SVM的转化过程就是建立一个非线性映射Φ ，将数据χ映射到高维特征空间F，回归函数为[9]：

根据多元统计分析理论，可通过以下目标数极小化确定SVM回归函数：

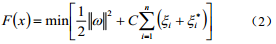
约束条件为：

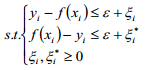
拉格朗日对偶性变量约束优化：

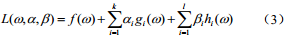
约束条件为：

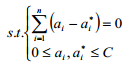
式（1）—（4）中：α i,α i—拉格朗日系数； 

                  αi， β i—拉格朗日算子； 

                  b—临界值； 

                 ω—权值矢量； 

                 ξ ,ξ*—非负松弛变量； 

                 С—惩罚变量； 

                ε—不敏感损失函数参 数； 

                Κ (χi,χj)—SVM的核函数。

核函数是计算两个向量在隐式映射空间中的内积函数，将低维空间中向量通过变换得到高维空间量的向量内积值，文中选用高斯径向基核函数，即：K（xi，xj）=exp（-g|xi-xj|2），g为核函数的参数宽度。

通过以上的理论推导可得到回归函数为：

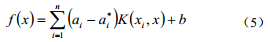
对于新的输入参数x可通过该式计算得到相应的输出值。

2 果蝇算法优化支持向量机

果蝇优化算法是一种基于果蝇觅食行为而推演出寻求全局群智能优化的新方法，属于演化式计算的范畴，亦属于人工智能的领域，可混合其他方法与管道内腐蚀技术一起使用，如模糊数学、经验公式、灰色系统与神经网络等。通过果蝇自身位置来估计周围的味道浓度，随后果蝇向味道浓度的极值方向飞去，重复迭代味道浓度求取目标函数的最优解[12-14]。

由于果蝇是在三维空间飞行，而原始的FOA算法是在二维空间搜寻全局极值，因此将可能导致无法搜寻到三维空间中的最佳值，因此本文采用三维空间搜寻，对FOA进行改进。

FOA对SVM优化的具体步骤，见图 1所示。

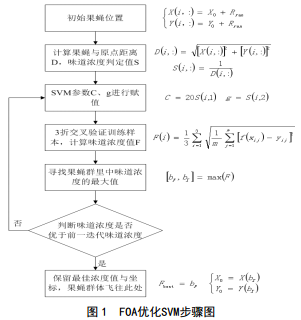
图 1式中：Rγαn —随机数；i＝1,2，…m；yij—真实值；m—各个交叉验证训练子集的果蝇数目；f（χij）—交叉训练的预测值；bF-F的最大值；bI-F最大值所处的位置。

因为SVM的优化参数是С和 g，所以 X 和 Y 均为m 行2列矩阵。采用迭代的方法对参数进行优化，同时判定味道浓度相比上一次迭代的味道浓度变化，如果优于上一步迭代则转至步骤（7），否则继续循环直至达到指定循环次数N时，循环终止。

3 FOA-SVM管道内腐蚀速率预测模型

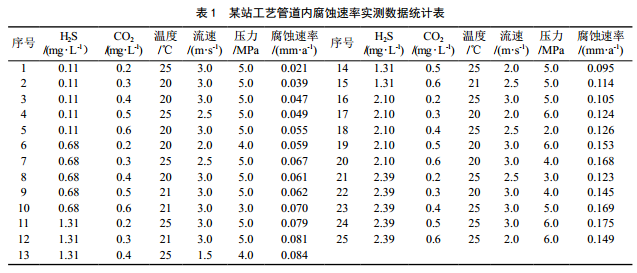
某站管道材质为20#钢， 2003年10月建成投产，使用压力为4～7 MPa，输送介质为天然气，影响管道内腐蚀速率主要参数为H2S、 CO2、温度、流速、压力，实测数据统计见表 1。将影响内腐蚀速率的参数作为输入向量，内腐蚀速率作为输出向量，建立FOA-SVM预测模型。选取某输油站管道内腐蚀速率实测数据1～25组样本作为训练集，以某站实验数据作为测试集，采用实测值与灰色马尔科夫组合模型、BP神经网络模型、 FOA-SVM模型预计值对比分析的方法，对FOA-SVM模型的性能进行评价。

3.1 建立回归模型

将参数值输入SPSS软件，设腐蚀速率y 为因变量，硫含量χ 1、酸值χ 2、温度χ 3、流速χ 4、压力χ 5为自变量。 FOA-SVM多元线性回归模型采用逐步回归的方法，针对影响因素变量对因变量的影响程度进行分析比较。建立多元性回归模型时，为了使得回归模型具有良好的解释能力和预测效果，自变量的选择准则为：

（1）自变量对因变量呈线性相关，且影响效果显著；

（2）相关程度比较，自变量之间应低于因变量与自变量之间的的相关程度；

（3） 预测值的确定，自变量应完全满足因变量的统计数据。

优选自变量过程中，当回归方程中所有自变量对因变量各自影响显著时，再考虑从其他未选中变量代人方程，循环往复直至所有自变量优选后，求解结束。由逐步回归法得到的回归方程为：

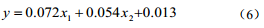
由此可以看出，逐步回归忽略了温度、流速两个变量，压力对管道的腐蚀速率影响不大。而回归方程中硫含量和酸值的Sig值都为0，具有统计显著性。得到的回归方程的调整R 方为0.307，具有较好的拟合优度。

对模型所有数据进行残差分析，优化模型。结果显示6、 8、 9号三组数据的残差绝对值残差较大，忽略这三组数据，重新建立回归方程，调整R 方为0.426，满足要求。得到结果为：

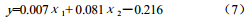
3.2 腐蚀速率预测及分析

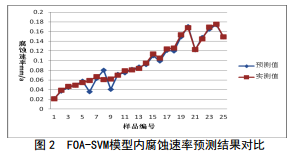
基于FOA模型优化回归参数C 和g ，设定群体个数为25，遗传代数为200， C参数范围[0,500]， g参数范围[0,100]。得到的优化参数C1和g1为0.041和0.0128输入FOA-SVM模型训练，结果见图 2。图 2中除6、 8和9三个样本外，其他训练后的样本和实测值具有很好的拟合性。

3.3 FOA-SVM模型评价

为了体现FOA-SVM模型的优越性，使用某输油管道实验数据对FOA-SVM模型进行检验，将其结果与灰色马尔科夫组合模型[4]、 BP神经网络模型[5]两种方法计算结果进行比较，见表 2。

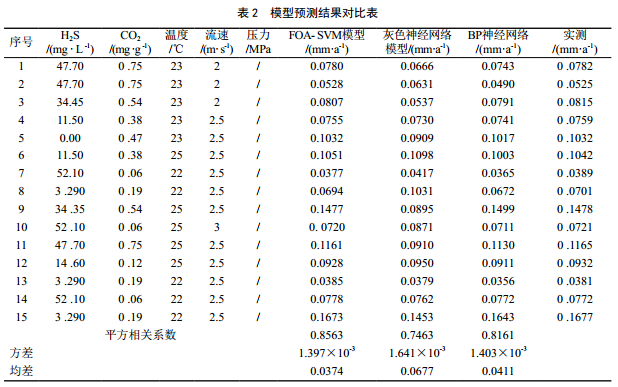
从表 2中知， FOA-SVM预测模型预测结果的方差和均差分别为0.0374、 1.397×10-3，从误差角度分析来看， FOA-SVM 模型预测值方差、均差都小于其他算法，说明FOA-SVM 模型具有相对较高的预测精度；从拟合效果来看， FOA-SVM 模型的平方相关系数高于其他模型，说明FOA-SVM 具有较好的拟合效果。

4 结论

（1）运用新建的FOA-SVM模型对天然气场站工艺管道内腐蚀速率进行了预测该模型预计的方差为1.397×10-3，均差为0.0374，并与灰色马尔科夫组合模型 、 BP神经网络模型预测结果的对比分析，具有较好的泛化能力和较强的预测功能，可以相对准确、高效地对输油管道内腐蚀速率进行预测。

（2）FOA-SVM模型算法充实了管道内腐蚀速率的预测方法，虽然能够准确、高效预测管道内腐蚀速率，但该模型针对样本数目多时，存在训练消耗时间长、效率低的缺点，今后在预测效率问题上还需进一步研究。

参考文献：

[1]陈浩力,吕仁军,姜炜,李尚泽,等. 基于Excel的GM(1,1)模型在预测油气管道腐蚀速率中的应用[J]. 腐蚀与防护,2014,04:378-380.

[2]刘晓东,李著信. 基于灰色组合模型的管道腐蚀速率预测[J]. 压力容器,2007,03:15-19.

[3]王晓光,张弢,周慧. 基于LS-SVM的管道腐蚀速率灰色组合预测模型[J].数学的实践与认识,2014,07:82-87.

[4]张宏伟,朱志洁,霍丙杰,等.基于改进的FOA-SVM导水裂隙带高度预测研究[J].中国安全科学学报,2013,10:9-14.

[5]陈永红,张大发,王悦民,彭桂初.基于灰色马尔科夫组合模型的管道腐蚀速率预测方法[J].核动力工程,2009,30(02):95-98.

[6]胡松青,石鑫,胡建春,任振甲,郭爱玲,高元军.基于BP神经网络的输油管道内腐蚀速率预测模型[J]. 油气储运,2010,29(06):448-450+398.

[7]丁世飞,齐丙娟,谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011,01:2-10.

[8]顾亚祥,丁世飞. 支持向量机研究进展[J]. 计算机科学,2011,02:14-17.

[9]张学工．关于统计学习理论与支持向量机[J]．自动化学报， 2000,26(1)： 32-43．

[10]Pan Wentsao. A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-Based Systems, 2011,26(7):69-74.

[11]牛培峰,麻红波,等. 基于支持向量机和果蝇优化算法的循环流化床锅炉Nox排放特性研究[J]. 动力工程学报,2013,33(4):267-271.

[12]张勇,夏树发,唐冬生. 果蝇优化算法对多峰函数求解性能的仿真研究[J]. 暨南大学学报(自然科学与医学版),2014,01:82-87.

[13]宁剑平,王冰,李洪儒,许葆华. 递减步长果蝇优化算法及应用[J]. 深圳大学学报(理工版),2014,04:367-373.[14]高东磊,刘友宽,苏杰,等. 果蝇优化算法和粒子群优化算法的应用对比[J].仪器仪表用户,2013,04:83-84+41.

作者：王志月， 1985年生，中石油管道有限责任公司西气东输分公司规划计划处， 2009年毕业于北京航空航天大学技术经济及管理专业。现主要从事油气管道项目后评价及计划管理工作。