毛瑞麒1 饶连涛1 刘觉非2 苏林2 成文峰2 徐杰1

1.中国矿业大学 材料与物理学院；

2.国家管网集团东部原油储运公司管道检验检测中心

摘要：基于漏磁检测技术基本原理，采用有限元方法对管道腐蚀凹坑的漏磁场进行了仿真模拟，得到不同提离值下的磁通密度径向分量峰值，基于L-M拟合分析获得了拟合参量，同时运用BP神经网络算法，构建了缺陷参数和拟合参量之间的关系。结果表明：相同提离值下，随凹坑直径减小或深度增加，漏磁信号均增大，且直径越小，深度越大，漏磁信号衰减速率越快。BP神经网络可以很好地构建拟合参量与缺陷参数之间的映射关系，从而为缺陷量化分析提供了新的思路。

关键词：漏磁信号；提离值；指数拟合；拟合参量；BP神经网络算法

漏磁检测是管道无损检测最常见的方法之一，具有对管道内环境要求不高、无需耦合、价格低廉等优点[1,2]。但管道缺陷量化分析是目前漏磁检测技术的难点，只有保证对缺陷参数的精确量化，才能对管道的安全性进行准确评估[3]。

本文基于管道漏磁检测技术基本原理，采用有限元方法，针对不同尺寸腐蚀凹坑缺陷的漏磁场进行三维建模与仿真模拟，通过提取不同提离值下磁通密度径向分量峰值并进行L-M拟合分析，同时，采用BP神经网络算法构建缺陷参数与拟合参量之间的映射关系，从而进行缺陷量化分析。

1  漏磁检测基本原理及有限元模型

1.1  漏磁检测基本原理

图 1给出了漏磁检测基本原理示意图[4,5]：磁化器中的永磁铁产生磁场，并通过极靴、衔铁和管道形成完整的磁回路。由于管材的磁导率远大于空气，当管壁无缺陷时，通过管道的磁感线大多被约束在管壁内部。而当管道出现凹坑、裂纹等切割磁力线的缺陷时，由于缺陷处磁阻远远大于管材，会使部分磁感线从管壁漏出，形成漏磁场，可被管道上方的磁敏感传感器接收，通过检测到的相关信号的变化，可对缺陷的几何特征及位置进行分析与判别。

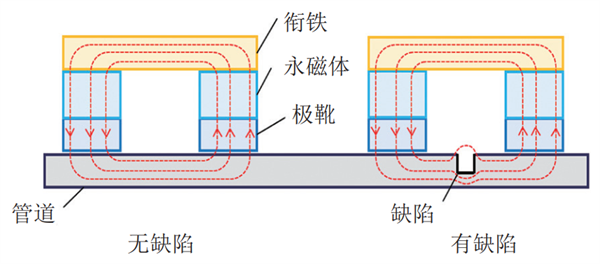
图 1 漏磁检测基本原理示意图

1.2  漏磁检测有限元模型

采用COMSOL软件来模拟漏磁检测过程，结合文献[6,7]中的研究和实际检测装置，建立了如图 2所示的有限元模型及网格划分。为简化模型，这里采用平板代替管子，并在外围构建空气罩模拟磁场在空气中的分布情况。缺陷Ω采用半椭球凹坑来表征，缺陷参数分别为凹坑直径L和凹坑深度D，即一个管道缺陷可表示为Ω（D， L）。表 1给出了模型中各部件材料属性、磁化方式以及边界条件定义。

（a）有限元几何模型

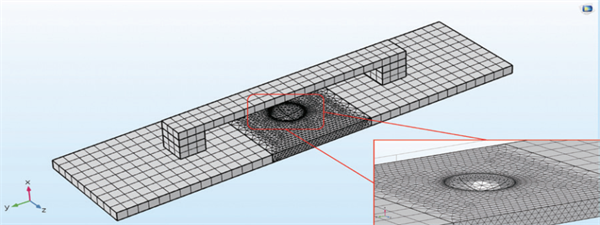
（b）有限元网格划分
图 2 凹坑缺陷模型及网格划分

表 1 模型各部件材料属性及边界条件

2  基于L-M优化的Bx_max-H指数拟合

2.1  漏磁信号随提离值的衰减规律

在实际检测过程中，由于管壁的腐蚀、剥落以及检测装置行进时自身产生的振动等因素，常会导致传感器提离值发生变化，从而对检测结果造成较大的影响。为研究提离值对漏磁信号的影响规律，针对直径30 mm、深度5 mm的缺陷漏磁场分布特征进行仿真模拟，得到不同提离值下磁通密度径向分量分布曲线，如图 3所示。同时，提取图 3中径向分量峰值Bx_max，并绘制得到Bx_max随提离值高度H的变化曲线，如图 4所示。

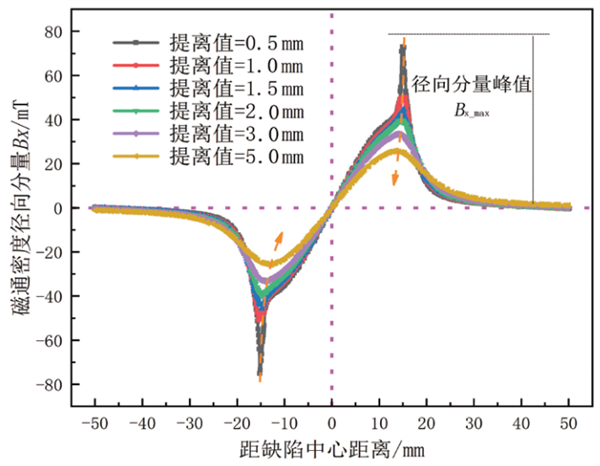
图 3 不同提离值下磁通密度径向分量分布曲线

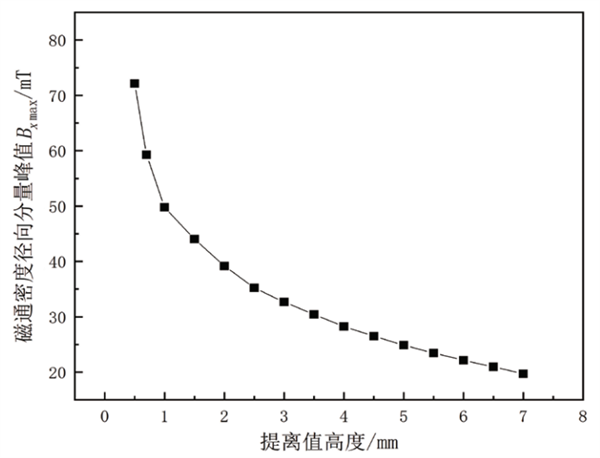
图 4 不同提离值时磁通密度径向分量的峰值

从图 3可以看出，随着提离值的增高，磁通密度径向分量明显降低。这是由于空气中磁阻较大，磁力线趋向于从磁阻小的管壁内通过，提离值越高，距离管壁越远，磁力线分布越稀疏，故而磁通密度越小。同时，由图 4结果可以看出：磁通密度径向分量峰值（取值方法如图 3所示）随提离值增高呈非线性衰减趋势，且在提离值较低时，衰减速率较快，随提离值增高，衰减速率逐渐变缓，该结果与文献[8]中的结果是一致的。

2.2  基于L-M优化的Bx_max-H指数拟合

采用指数函数y＝α1+α2eα3χ对不同缺陷的Bx_max-H的衰减规律进行拟合分析。同时，由于L-M算法是一种利用梯度求最值的最优化算法，因此，采用L-M优化的迭代最小二乘法来估计不同缺陷参数下的拟合参量α1、α2和α3的值，得到Bx_max-H关系曲线及其拟合结果（部分）如图 5所示，可见，曲线整体拟合结果非常好。

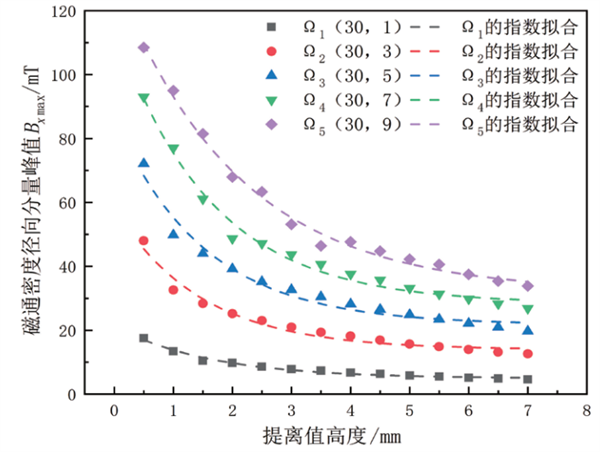
图 5 Bx _max-H关系图及其指数拟合曲线（部分）

3  基于BP神经网络算法的缺陷反演

3.1  BP神经网络算法基本原理

神经网络技术是近年来发展起来的一门交叉学科，其具有非线性映射、分布并行处理和自适应学习等特性，是一种具有三层或三层以上节点的单向传播的多层前馈网络[9]。其基本结构主要分为三层（图 6）：输入层、隐藏层和输出层。每层具有n个节点，每个节点上的值将通过前一层各个节点的数据经过加权求和以及非线性运算得到[10]。通过对比神经网络输出层得到的预测值和真实值之间的差异，以最小误差来反向更新每个连接的权重和偏向。每个训练实例进行一次该操作，当所有输入的训练实例使用完毕后，可得到一个误差最小的权重和偏向，即一个训练好的神经网络其实是一个权重和偏向全部更新完毕后的神经网络。文中分别将指数拟合和幂函数拟合的回归系数作为输入量，将缺陷参数（直径L和深度D）作为输出量，采用BP神经网络算法进行训练。

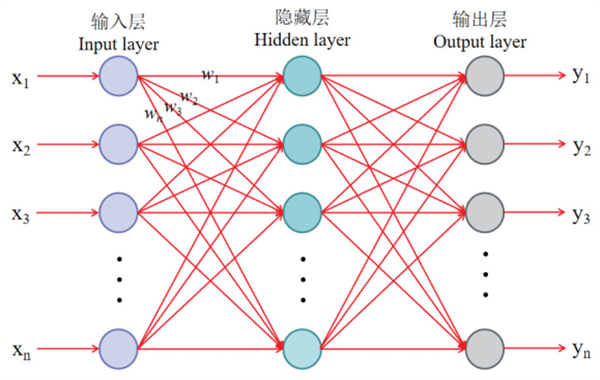
图 6 神经网络基本结构

3.2  基于BP神经网络算法进行缺陷量化分析的计算流程

缺陷量化分析指根据已知的漏磁信号分析缺陷的各项参数信息[11,12]，也称缺陷反演。通过以上分析可以看出，在磁化器和管壁厚确定的情况下，提离值衰减曲线的拟合方程系数和缺陷参数之间存在映射关系。即若已知提离值衰减曲线的系数，亦可反推出缺陷的相关参数，其计算流程如图 7所示。

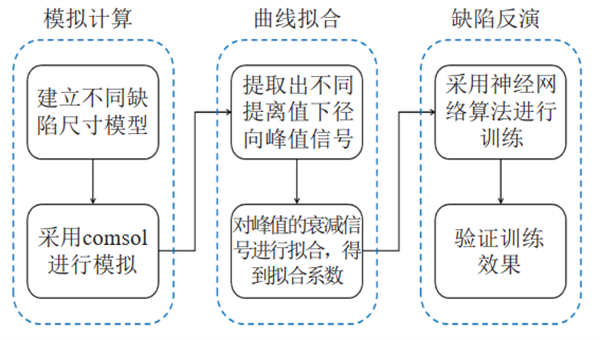
图 7 基于BP神经网络进行缺陷反演的计算流程

3.3  BP神经网络算法训练及验证

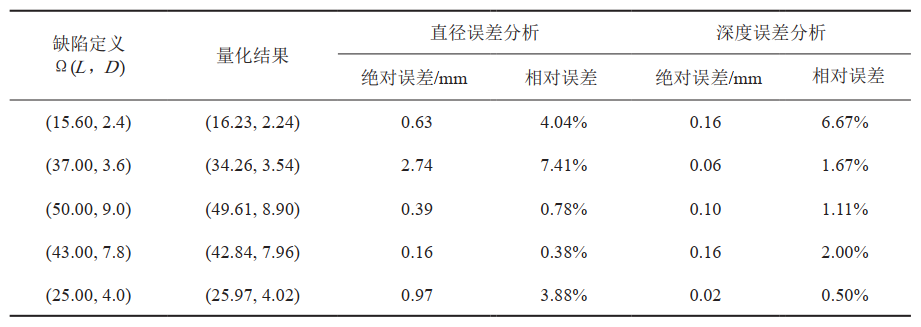
文中共对81组不同几何参数缺陷的漏磁信号随提离值增大的衰减曲线作为样本进行了计算，训练完毕后对样本组缺陷进行反演，得到结果如图 8所示。

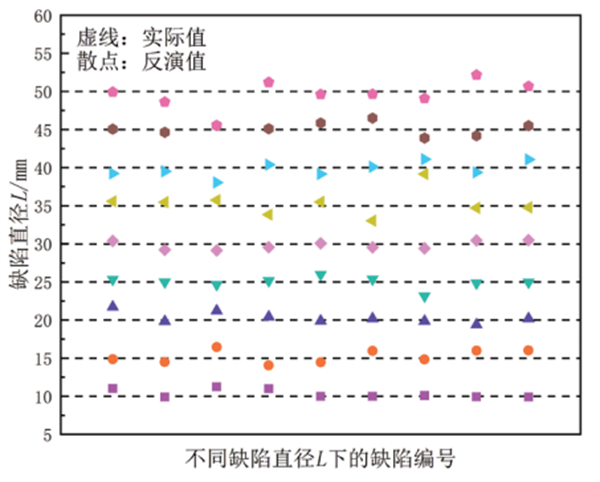
（a）缺陷直径反演结果

（b）缺陷深度反演结果

图 8 基于神经网络算法的缺陷反演结果

图 8中虚线表示缺陷的实际尺寸，样本点表示通过神经网络算法进行缺陷反演得到的缺陷尺寸。由结果可以看出，本文的反演方法可以准确地量化缺陷尺寸，相对误差几乎都在10%以下，绝大部分误差在5%左右。同时，为进一步验证此反演方法的可靠性和准确性，本文随机选取了5组缺陷带入训练结果进行反演，得到结果如表 2所示。可见，本文提出的缺陷量化方法精确度较高，可为实际工程中缺陷反演提供新的思路和理论支持。

表 2 随机缺陷反演分析验证结果

4  结论

基于漏磁检测技术原理，采用COMSOL软件对腐蚀坑缺陷的漏磁信号特征进行了仿真模拟，并基于L-M拟合和神经网络算法对缺陷进行了量化分析，结果表明：

（1）凹坑直径越小、深度越大，磁通密度径向分量峰值 Bx_max随提离值增高的衰减速率越快。

（2）指数拟合可以较好地表征磁通密度径向分量峰值Bx_max随提离值增高而衰减的变化趋势。

（3）通过BP神经网络算法构建提离值衰减曲线的拟合参量与缺陷参数之间的关系，可对缺陷进行准确预测，为实际工程中缺陷反演提供了一种新的方法。

 

参考文献：

[1]S Miller, F Sander. Advances in feature identification using tri-axial MFL sensor technology[C]. Proceedings of Pipeline Technology Conference, Hannover Messe, Hannover, German, 2008.

[2]杨理践，耿浩，高松巍.长输油气管道漏磁内检测技术[J]. 仪器仪表学报，2016，37(8)：1736-1746.

[3]苏林，马雪莉，成文峰. 管道漏磁内检测量化方法研究[J]. 安全、健康和环境，2020，20(7)：35-37，43.

[4]曹辉，杨理践，刘俊甫，等. 基于数据融合的小波变换漏磁异常边缘检测[J]. 仪器仪表学报，2019，40(12)：71-79.

[5]刘刚. 管道漏磁内检测关键技术问题研究[D]. 沈阳：沈阳工业大学，2010.

[6]苏林，成文峰，刘保余. 管道环焊缝缺陷漏磁检测信号仿真分析[J]. 焊接，2020(3)：10-16.

[7]毛瑞麒，马梦想，饶连涛，等. 管道环焊缝缺陷漏磁检测仿真模拟[J]. 电焊机，2020，50(11)：28-36+143.

[8]李二龙. 基于提离值测量的钢管漏磁检测信号动态补偿方法[D]. 武汉：华中科技大学，2014.

[9]邱忠超，张卫民，张瑞蕾，等. 基于改进BP神经网络的微裂纹漏磁定量识别[J]. 东北大学学报(自然科学版)，2016，37(12)：1759-1763.

[10]张争，马杰，刘永智，等. 基于BP神经网络的隧洞围岩参数反演[J]. 西北水电，2021(02)：55-58.

[11]刘斌，杨理践. 长输油气管道漏磁内检测技术[M]. 北京：机械工业出版社，2017.

[12]李岩松，王麒翔，王敏壕，等. 漏磁检测的混合正则化反演方法研究[J].电测与仪表，2020，57(21)：9-17.

 

作者简介：毛瑞麒，中国矿业大学材料与物理学院本科生，主要研究方向为管道漏磁检测及有限元模拟。

通讯作者：徐杰，女，博士，副教授，主要从事金属焊接结构断裂、疲劳，管道检验检测、管线钢结构完整性评估和有限元数值模拟等方面的研究工作。联系方式：15162158467，j.xu@cumt.edu.cn。