赵飞
四川长宁天然气开发有限责任公司

摘要：通过动水阻力系数和经验公式计算涡流释放频率，再以管道自振频率与涡流释放频率的关系作为避免发生涡激共振现象的条件，求解临界自振频率。最终得出SZ36-1CEP至绥中终端海底管道悬空段在不同支撑形式下的临界跨长值。利用ANSYS有限元软件建立双层管简化模型并对不同支撑形式下的应力应变进行分析。结果表明，在管道悬空段的中间节点处应力达到最大值，简单支撑比固定支撑条件下的管道变形大。

关键词：海底管道；涡激振动；支撑条件；临界跨长；有限元分析

SZ36-1CEP至绥中陆地终端海底管道东起辽东湾中部，向西延伸至绥中县万家屯乡高岭村的陆地终端登陆，管线全长69.47 km。目前海底管道悬跨段的安全评估主要通过求解涡激振动方程[1]、应用ANSYS有限元分析软件计算或者通过实验进行分析。笔者通过海底管道悬空段在水流作用下引起的振动效应，即根据涡流释放频率（涡流频率）推导出避免发生涡激振动的管道自振频率[2]，再根据管线自振频率与悬空管段之间的关系求出最大临界跨长。

1  理论分析与计算

1.1  涡激振动

管道涡激振动会导致深海中平管和立管发生响应振动和疲劳破坏，从而增大管道失效概率，缩短管道使用寿命[3]。管道振动出现在横流方向上的可能性较大[4]，一般认为顺流方向的振动不会引发严重的管道振动问题，图 1表示涡流引起的振动。

图 1 涡流引起的振动

1.2  基础参数

涡流释放频率由式（1）表示[5]： 

式中fs为涡流释放频率，Hz；St为斯托劳哈尔（Strouhal）数；Uc为流经管道中心位置的潮流速度（假定为稳定流或恒流），m/s；Do为管道外径，m。流动雷诺数Re由式（2）表示： 

式中ue为管道高度上有效的水平水粒子速度，m/s；ν为流体的运动黏度（海水约9.3×10-7  m2/s），m2/s。斯托劳哈尔数St是Re的函数，阻力系数也是Re的函数，这样可以根据水流在管道周围的Re，由图 2查得St。 

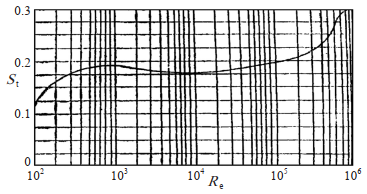
图 2 斯托劳哈尔数St与流动雷诺数Re的关系曲线

根据霍尔纳（Hoerner）经验关系式（3）也可求得St：

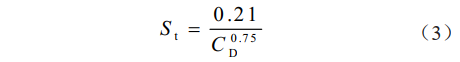
式中CD为动水阻力系数。

1.3  管道自振频率

通过Bernoulli-Euler单跨梁横向振动方程、海底悬空管段支撑方式（简单支撑、固定支撑）的临界条件分析以及推导得知，海底悬空管段的固有频率（自振频率）通式（4）为： 

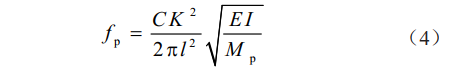
式中fp为海底悬空管段的固有频率，Hz；C为系数（水中振动取0.7，空气中振动取1.0）；K为系数；ι 为海底悬空管段跨长，m；I为管道断面的惯性矩（双层管可按复壁钢管计算），m4；E为管材弹性模量，E＝210 GPa；Mp为海底管道单位长度质量，kg/m。K为与海底悬空管段两端支撑条件有关的系数，两端固定连接（固定支撑）时 K=3/2π=4.73；两端铰支连接（简单支撑）时K=π=3.14；一段铰支、另一端固定连接时按简单支撑计算。

1.4  避免涡激共振的临界条件

一般认为fs＝（0.8～1.2）fp，海底悬空管将会出现涡激共振现象[6]，由式（1）可知，已知海底悬空管段CD为定值，则St也为定值，Uc、Do为已知定值，所以fs就是定值。因此，避免发生涡激共振现象的主要措施是改变fp大小，从式（4）可以看出，改变fp最有效的方法是控制海底悬空管段的跨长，从而避免出现涡激共振现象。

1.5  悬空管段临界跨长

实际工程中，fp≥10fs，可以认为不会发生涡激共振[7]，即为海底管道临界固有频率值。由此得出海底管道临界悬跨长度公式（5）[8-9]：

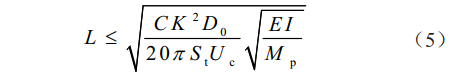
2  应用实例

2.1  已知数据

SZ36-1CEP至绥中陆地终端海底管道悬空段如图 3所示。

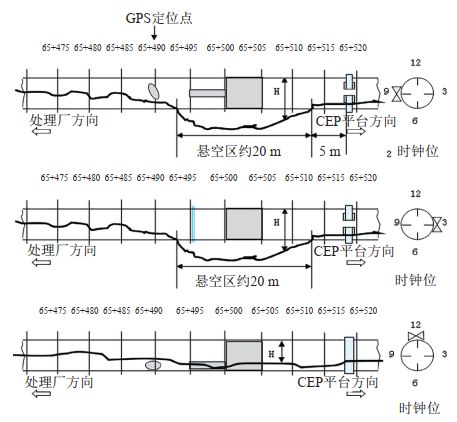
图 3 SZ36-1CEP至绥中终端管线悬跨示意图

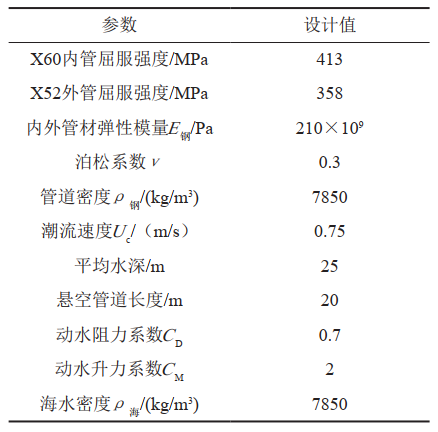
该管道为双层保温管结构，计算参数根据工程设计参数选取，物理参数如表 1所示；运行参数为50℃时输送油品密度ρ油＝949.5 kg/m3；其他设计参数如表 2所示。

表 1 SZ36-1CEP至陆地终端海底管道物理参数表（ mm）

表 2 SZ36-1CEP至陆地终端海底管道工程设计参数

2.2  计算过程

2.2.1  斯托劳哈尔数

（1）基于St和Re函数关系，已知ue为0.75 m/s；Do为0.6604 m；海水的运动黏度ν为9.3×10-7  m2/s，则：

据此查得斯托劳哈尔数St＝0.262。

（2）基于式（3），已知CD＝0.7，则：

两种方法得出的结果相差不大，最终取St为0.27。

2.2.2  涡流频率

已知St＝0.27；Uc＝0.75 m/s；Do＝0.6604 m，则涡流频率fs为：

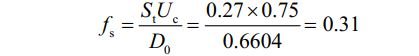
2.2.3  临界自振频率

已知fs＝0.31 Hz，则避免海底管道悬空段出现涡激共振的临界自振频率fp＝10 fs＝3.1 Hz。

2.2.4  悬跨管道的刚度

该悬空管段惯性矩包括内钢管惯性矩I内和外钢管惯性矩I外，可根据软件CAD自动计算或由式（6）计算，即： 得出I内＝5.8×10-3m4；I外＝1.7×10-2m4；钢管弹性模量E＝210×109 Pa；则管道的总刚度：

（EI）总＝（EI）内+（EI）外

（EI）总＝210×109×5.8×10-3+210×109×0.017＝4.788×109Pa·m2

2.2.5  单位长度质量

海底悬空管段的单位长度质量包括输送流体质量、内管质量、保温层质量、外管质量、附加质量（一般可取管道排开水体积的1～2倍）。分别计算M流体、M内管、M保温、M外管、M附加，相加得出海底管道的单位长度质量MP。

2.2.6  临界跨长

由于悬空管段整体在水中振动，所以统一取C＝1.0。

（1）海底悬空管道两端为固定支撑

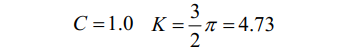
将两个参数代入式（5）中，可得：

 （2）海底悬空管道两端为简单支撑

C＝1.0   K＝π＝3.14

则：

3  有限元分析

3.1  参数简化处理

在ANSYS软件中，为了简化计算[10]，将双层管简化成单层管，按单位长度质量和管道刚度相等的原则，利用双层管道复合截面的刚度，来确定简化后的单层管道内的壁厚和其有效密度。为保证简化之后的管道受力不变，简化后的管道外径保持不变。

保温层的有效载荷仅约1%，且其弹性模量相对其他层很小，相比之下防腐层较薄，所以防腐层和保温层对刚度的影响忽略不计。

双层管截面刚度：

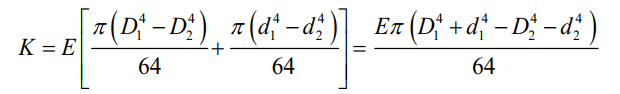
式中D1为外管外径，m；D2为外管内径，m；d1为内管外径，m；d2为内管内径，m； 假设简化后的单层管道内径为r，简化后的管道内壁厚为δ，简化前后外径和总刚度不变，则：

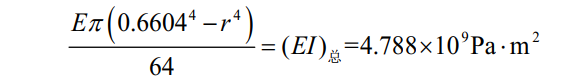
计算得r＝627.1 mm，δ＝（660.4-627.1）/2 ＝16.7 mm。简化后单层管的有效密度为ρ有效，简化前后管道单位长度质量不变，则：

计算得ρ有效＝27411 kg/m。

3.2  几何模型

图 4为海底管道悬空段固定支撑的立体应力分布和变形图[11]，其最大应力出现在管道支撑两端，最大值为89 MPa。忽略支撑端的应力集中现象，其悬空管段中间节点最大应力值为30 MPa，最小应力为0.1065 MPa，最大变形量为10.5 mm。

图 4 海底管道悬空段固定支撑应力分布和变形图

  简单支撑悬空管段最大应力出现在管道的中间节点，最大值为86.9 MPa，最小应力为0.4193 MPa，最大变形量为400 mm；如图 5所示。

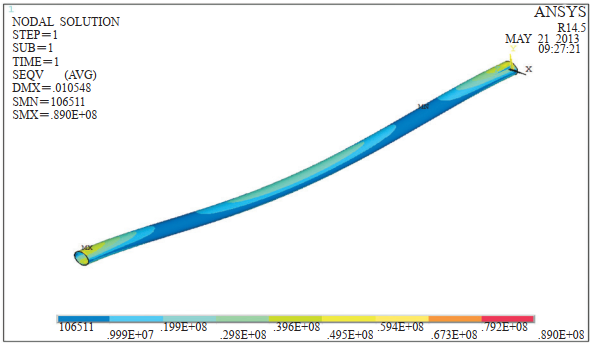
图 5 海底管道悬空段简单支撑应力分布和变形图

  4  结论

  （1）SZ36-1CEP至绥中终端海底悬跨管道两端为简单支撑时，最大临界跨长为28.4 m；最大应力为86.9 MPa，出现在管道的中部位置；最大变形为400 mm。

  （2）管道两端为固定支撑时，最大允许跨长为42.6 m；最大应力为89 MPa，出现在管道的支撑两端；管道中间最大应力为30 MPa，最大变形为10.5 mm。

  （3）实际工程中，建议采用较为保守的最大允许跨长值，即临界跨长28.4 m。目前SZ36-1CEP至绥中终端海底悬跨管道悬跨长度为20 m，处于安全状态。

参考文献：
[1]李小超，王永学.基于频率响应法海底悬跨管涡激振动分析[J].海洋工程，2009(04)：31-37 .

[2]杨兵，高福平，吴应湘.单向水流作用下近壁管道横向涡激振动实验研究[J].中国海上油气，2006(01)：52-56.

[3]孟昭瑛，杨树耕，王仲捷.水下管道涡激振动的实验研究[J].水利学报，1994(07)：43-50.

[4]马良.海底管道在水流作用时诱发的振动效应[J].中国海洋平台，2000(02):30-34.

[5]娄敏.海底管道悬跨段涡激振动动力特性及动力响应的数值模拟[D].青岛：中国海洋大学，2005.

[6]余建星，孙凡，傅明炀，杜尊峰，郭君.海底管线涡激振动响应动力特性[J].天津大学学报，2009(01) :1-5.

[7]董丽丽，徐慧，郭振邦.海底管道悬跨长度的计算[J].中国海上油气工程，2003，15(6)：16-18.

[8]陈博文，孙丽，谷凡.海底管道最大允许悬跨长度计算[J].防灾减灾工程学报，2003，9(30)：291-293.

[9]余建星，马勇健，杨源，张英，方伟，刘凯.海底管道允许悬空长度计算研究[J].天津理工大学学报，2014，2(30)：6-10.

[10]隋之锋，郝点，陈海峰.ANSYS在两端固定厚壁管道应力分析中的应用[J].贵州化工，2008(06) ：34-37.

[11]刘纯，胡波涛.应用ANSYS计算汽水管道应力[J].锅炉技术，2005(04)：31-33.

  

  作者简介：赵飞，1992年生，工程师，本科，毕业于西南石油大学，主要从事压力管道、容器定期检验、合于使用评价、管道完整性管理相关的研究与应用工作。联系方式：18728499960，294778388@qq.com。