崔雪萌 杨昕谅 张演义 郝卓卓 白保存

北京管道陕西输油气分公司

 

摘要：压缩机是天然气压气站的核心设备，也是耗能最多的设备。优化压缩机运行方案、降低能耗对降低管道生产运行成本以及减少碳排放有重要意义。以能耗最小为目标，针对压气站压缩机运行提出了一个优化模型，基于气体流动方程和压缩机特性方程，使用主流求解器GUROBI进行求解。采用某压气站实际生产数据验证了模型的有效性，为调整机组运行方案提供理论依据。

关键词：天然气管道；压缩机；运行方案优化；特性预测；非线性优化

 

北京管道榆林压气站是陕京二、三线的第一座压气站，拥有5台变频电机驱动离心式压缩机和3台燃气轮机驱动的离心式压缩机，站内变频电机的用电量占总用电量的80%以上，燃气轮机的用气量占总输气量的0.3%以上。因此优化压缩机的能源消耗对降低管道运行成本以及减少碳排放有重要意义。压气站机组运行决策（机组的启停、转速等）由站内值班人员根据国家管网集团油气调度中心下发的调度指令，结合实际情况制定，具有一定随机性。本文以能耗最小为目标，针对压缩机运行提出了一个优化模型，决策变量来自压缩机运行方案，一系列约束条件基于气体流动方程和压缩机特性方程。由于约束条件存在非线性的二次约束，提出的模型为二次优化模型(Quadratic Program，QP)。使用主流求解器GUROBI进行求解。算例分析部分用压气站实际生产数据验证模型的有效性。

1  国内外优化研究概述

目前国内外针对天然气管网的优化大体上分为设计优化和运行优化两类[1]。前者主要针对管网系统结构设计、管道材料选择、压气站配置和选址进行优化[2]，优化目标有系统输气能力最大化[3]、运行灵活性最大化[4]、未来扩展能力最大化[5]以及投资最小化等。后者优化目标主要有操作成本最小化[6]、输气量最大化[7]、管道储气量最大化[8]、温室气体排放最小化[9]等。尽管研究众多，但其优化范围多针对管网系统，少有针对单一压气站的运行优化策略。本文提出的压缩机组运行优化模型基于目前的长输管道干线调度模式，针对性强，紧扣生产实际，更具指导意义。

2  模型建立

2.1  模型基础

本研究的主要目的是提出优化模型以确定拥有多台、多类型的并联压缩机的压气站最经济的压缩机运行方案。

（1）基础参数。①管网系统信息：压气站输气指定量（调度中心指令），压缩机进口压力（由上游来气压力决定），下游站进口压力（调度中心指令），到下游站距离，下游管道管材、直径、壁厚、粗糙度，地温；②设备信息：压缩机特性，驱动机效率。

（2）决策变量。①压缩机运行决策：不同时期机组运行方案（哪几台压缩机运行，每台压缩机的转速、流量等）；②设备能耗：不同时期压缩机组驱动机能耗。

（3）目标函数。在考虑各项物理量及工艺约束条件下，计算出某压气站不同时期的压缩机组运行方案，实现压缩机组能耗最小目标。

（4）模型假设。为方便建模并提高模型求解效率，提出了以下假设：①长输管道压气站运行时间被划分为一系列等长的离散单位时间；②该压气站到下游站之间的管道是水平管，天然气温度不变；③输气指定量、下游站进站压力已提前下达，在单位时间内不发生变化；④气源压力已知，且在单位时间内稳定，即压缩机入口压力在单位时间内为定值；⑤该压气站所有压缩机都并联，且忽略各压缩机入口压力因位置不同产生的差异；⑥所有压缩机工作过程均为绝热压缩，且都以厂家指导手册给出的实验特性运行。

2.2  模型变量与约束

模型中所涉及的已知参数均以小写字母组成的符号表示，变量均以大写字母开头的符号表示，参数和变量的单位备注均与后文算例所采用的单位一致。

（1）模型参数。数据集合、模型参数分别见表 1、表 2。

表 1 数据集合

表 2 模型参数

（2）变量定义。参数分别见表 3。

表 3 变量定义

（3）目标函数。以站内压缩机驱动机总功耗（ObjP）最小为目标函数，ObjP等于站内每台压缩机驱动机功率（Pqi,e）乘以运行时间之和，见式（1）：

（4）控制方程。根据管道流动方程、质量守恒原理、压缩机特性方程，建立了压气站压缩机与管网联合运行方程。

①管道流动方程：

根据假设，本压气站到下游站的管道为水平管道，水平管道水力计算公式及水力摩阻系数计算公式分别见式（2）、式（3）：

②压缩机方程：

离心式压缩机的能头及绝热系数计算分别见式（4）、式（5）：

压缩机能耗与驱动机能耗计算分别见式（6）、式（7）：

压缩机特性曲线是指在进气状态一定的条件下，转速、多变效率与进气量之间的关系，反映机组运行时工况的变化，通常用特性方程来表征特性曲线。离心压缩机的特性方程见式（8）、式（9）[10]：

压缩机转速在一定范围内，即nmin≤N≤nmax，喘振和阻塞约束见式（10）：

③管道与压缩机联合运行方程：

压缩机总输气量等于输气指定量，即Qct＝qt，由于所有压缩机并联，根据能量守恒定律，压缩机总输气量为每台压缩机输气量之和，见式（11）：

由于电机驱动的压缩机组启动前无需暖机，启动较快，为预防意外情况，日常运行中至少保留一台电驱压缩机备用。式（12）中Ee为电驱压缩机的编号集合，ne为电驱压缩机的台数：

3  算例分析

以榆林压气站实际生产数据为例，验证模型的有效性。优化模型使用Python编写程序，调用求解器GUROBI进行求解，并在4核8线程Intel CPU i7-6700（2.6 GHz）及16 GB内存的计算机上运行。

3.1  算例情况

压气站5台变频电机驱动的离心式压缩机和3台燃气轮机驱动的离心式压缩机，输气指定量以及压力控制值已提前下达，如图 1所示。

图 1 压气站月指定输气量

根据厂家提供的压缩机性能指标和测试数据，使用最小二乘法对压缩机特性曲线进行拟合。以电驱离心压缩机为例，拟合曲线如图 2、图 3所示，可以求出压缩机特性方程。

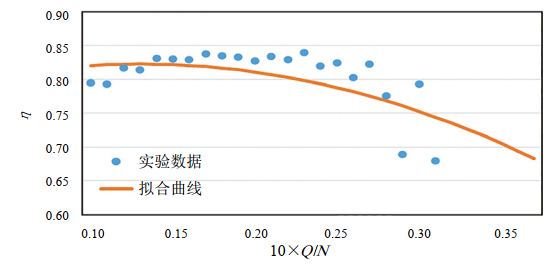
图 2 压缩机特性曲线拟合图

图 3 压缩机特性曲线拟合图

电动机的性能受环境影响较小，而燃气轮机的性能受环境影响比较大，温度升高热效率会下降，驱动机效率如图 4所示。

图 4 驱动机效率曲线

其他主要参数取值如表 4所示。

表 4 其他参数取值

3.2  计算结果

优化后得到了详细的压缩机组运行方案，如表 5所示，据此可以调整压气站压缩机组运行策略。例如，1月时，依据求得的转速，运行电驱1、3、4、5号机以及燃驱1、3号机最优。

表 5 优化后的压缩机运行方案

优化后机组总能耗与根据经验制定运行方案的机组总能耗对比如图 5所示，可以看出，合理决策压缩机的运行方案能够降低能耗，节省运行成本，减少碳排放。对现场调整机组运行方案具有指导意义。

图 5 压缩机能耗对比

3.3  敏感性分析

考虑到输气指定量、驱动机效率的不确定性，利用控制变量法进行了敏感性分析，以量化当其他参数保持在基准值时，每个单独参数对机组总能耗的影响。由图 6可以看出，机组总能耗与输气量呈正相关，与驱动机效率呈负相关，输气指定量对机组总能耗的影响较大，但驱动机效率的影响仍不容小觑。

图 6 敏感性分析

4  结论

（1）压气站机组运行有较大的优化空间，通过优化模型合理决策压缩机运行方案，可以节能降耗。

（2）驱动机效率对压缩机总能耗的影响不容小觑，有必要探究提高驱动机效率的措施。

（3）压缩机实际运行的特性曲线与厂家所提供的测试数据会因为入口状态、天气、海拔等原因存在一定的差异。为了更好地指导生产，有必要获取压缩机的实际特性曲线，未来可以考虑使用深度学习进行大数据分析，获得更为准确的压缩机特性曲线。

（4）由于压缩机特性曲线非线性程度高，求解器使用传统算法求解效率不够高，未来可以考虑使用遗传算法、粒子群算法等启发类算法进行求解。

 

参考文献：

[1]Demissie A , Zhu W , Belachew C T . A Multi-Objective Optimization Model for Gas Pipeline Operations[J]. Computers & Chemical Engineering, 2017, 100(may.8):94-103.

[2]Uester H , Dilaveroglu S . Optimization for design and operation of natural gas transmission networks[J]. Applied Energy, 2014, 133(nov.15):56-69.

[3]Alves F , JNMD Souza, Costa A L H . Multi-objective design optimization of natural gas transmission networks[J]. Computers & Chemical Engineering, 2016, 93(oct.4):212-220.

[4]Fodstad M , Midthun K T , Tomasgard A . Adding flexibility in a natural gas transportation network using interruptible transportation services[J]. European Journal of Operational Research, 2015, 243( 2):647-657.

[5]Mikolajkova M, Haikarainen C, Saxen H,et al. Optimization of a natural gas distribution network with potential future extensions[J]. Energy, 2017, 125(apr.15):848-859.

[6]Misra S, Fisher M W, Backhaus S,et al. Optimal Compression in Natural Gas Networks: A Geometric Programming Approach[J]. IEEE Transactions on Control of Network Systems, 2015, 2(1):47-56.

[7]Maryam,Fasihizadeh,Mohsen,et al. Improving gas transmission networks operation using simulation algorithms: Case study of the National Iranian Gas Network[J]. Journal of Natural Gas Science & Engineering, 2014,2:319-327

[8]Ernst M, Balestieri J, Landa H G, et al. Line-pack management for producing electric power on peak periods[J]. Applied Thermal Engineering, 2011, 31(1):42-49.

[9]BXYA,CHLB,BFW,et al.Impacts of emission reduction and external cost on natural gas distribution[J]. Applied Energy, 2017, 207:553-561.

[10]姬忠礼，邓志安，赵会军.泵和压缩机[M].北京：石油工业出版社，2008.

作者简介：崔雪萌，1995年生，硕士，助理工程师，2021年毕业于中国石油大学（北京），现从事长输管道运维以及自控与电气通信工作。联系方式：13241820426，1102463061@qq.com。