何礼元1 贾彦琨2 刘琨2 童骁2 梁伍1

1.北京中地华安环境工程有限公司；2.国家管网集团西气东输南昌输气分公司 

 

摘要：以某长输管道水毁地质灾害为研究对象，采用Logistic回归模型分别完成地质灾害易发性定量评价和影响条件地质灾害易发性定量评价，再综合两个定量评价结果获得最终地质灾害易发性定量评价结果，据此将研究区域地质灾害易发程度划分为高易发区、中易发区、低易发区和非易发区，对油气管道防灾减灾有一定指导意义。

关键词：油气管道；地质灾害；水毁；逻辑回归模型；易发性预测分区

 

我国长输油气管道沿线地质环境和自然条件十分复杂，部分地段地质灾害严重，对油气管道建设及运营构成较大制约和影响。根据近10年的统计，由地质灾害造成的油气管道运行失效约占11%，仅次于第三方施工损坏和打孔盗油破坏，严重威胁着管道的运行安全。

本文以某长输管道沿线为研究区，依据其年度地质灾害专业化排查出的地质灾害点及相关数据，根据野外调查数据分析地质灾害的发育条件、分布规律及致灾因素，选取有效的评价指标。采用逻辑回归模型构建易发性评价模型，预测灾害易发性概率。根据R方检验和显著性检验等结果判断模型精度和可靠性。最后对地质灾害易发区域进行划分，为油气管道沿线的减灾防灾及规划管理提供一定程度的参考。

1  Logistic回归模型介绍

Logistic函数由比利时数学家Pierre François Verhulst在1938年提出[1-3]，形式如下：

其中，N（t）表示t时刻个体数，r表示内在增长率，K表示承载力，化简为：

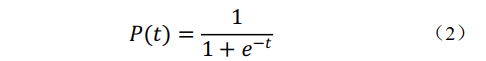
当因变量为二值变量时，0表示事件未发生；1表示事件发生。定义P为事件发生的概率，未发生即为1-P，把P看作为自变量Xi的线性函数。P对于Xi在P=0或P=1附近是不敏感且缓慢的，非线性程度较高，于是寻求一个关于P的函数，使得它在P=0或P=1附近变化幅度较大，引入Logistic函数变换，解得逻辑回归模型方程为：

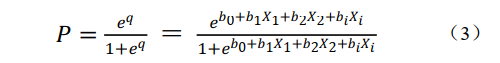
式中：P为研究区地质灾害发生概率；e为逻辑回归方程自然常数；b0为逻辑回归方程截距（逻辑回归方程的一个常数项）；bi（i＝1,2,3…,n）为逻辑回归模型中对应的评价因子Xi（i＝1,2,3…,n）的逻辑回归系数。

2  拟合分析

选取的指标有：高程X1、管道走向X2、积水影响长度X3、地表径流与管道关系X4、地形地貌X5、管道埋深X6。将数据带入Logistic回归模型进行拟合，其中地表径流与管道关系定义为分类变量，0表示否，1表示是。分类截止值设定为0.5。拟合后预测正确度统计如表 1所示，结果可知Logistic预测正确率高达81.1%，预测效果较好。

表 1 拟合优度统计量

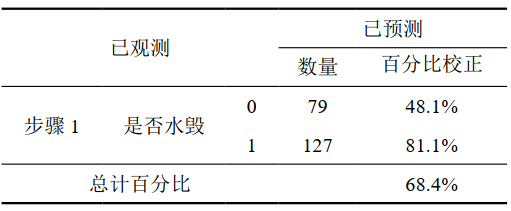
Cox & Snell R方和Nagelkerke R方检验结果参数表示模型的变量对因变量的解释能力，取值为0～1，越接近1解释能力越好。如表 2所示检验结果均大于0.5，说明具有较好的拟合程度。

表 2 拟合结果检验

拟合结果中自变量系数如表 3所示，B项为每个自变量所对应系数，S.E项为标准差，Sig项为显著性试验。在易发性评价过程中，逻辑回归模型运算结果中的B值为各评价因子对灾害发生的贡献度，其值越大说明该因子对灾害发生的影响越大。通过比较Wald和Sig值来判断各评价指标的显著性，Wald值越大或Sig值越小，显著性就越高。根据显著性检验结果，可以看出地表径流与管道关系、管道埋深等因素对灾害具有较高的敏感性。

表 3 自变量系数及结果检验

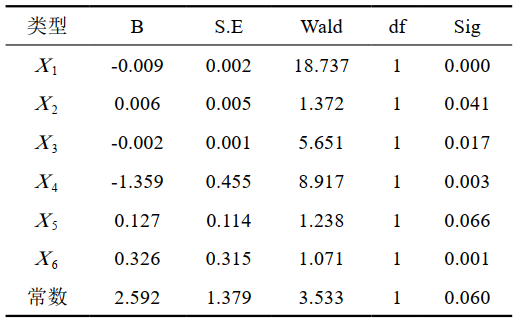
将常数、X1－X6自变量系数带入式（3），q＝2.592－0.009X1＋0.006X2－0.002X3－1.359X4＋0.127X5＋0.326X6。最终得出水毁灾害易发性概率计算模型如下：

3  易发性[4]概率预测

研究样本为某长输管道年度地质灾害专业化排查数据，地质灾害隐患点主要包括河沟道水毁、坡面水毁、台田地水毁等。野外调查时数据源采集参数包括里程、经度、纬度、高程、灾害点类型、土质类型、植被类型、管道走向、积水影响长度、地表径流与管道关系、地形地貌、管道状况、管道埋深等。如表 4所示，选取高程X1、管道走向X2、积水影响长度X3、地表径流与管道关系X4、地形地貌X5、管道埋深X6六个指标数据进行概率预测。

表 4 管道沿线现场原始数据（以10组数据为例）

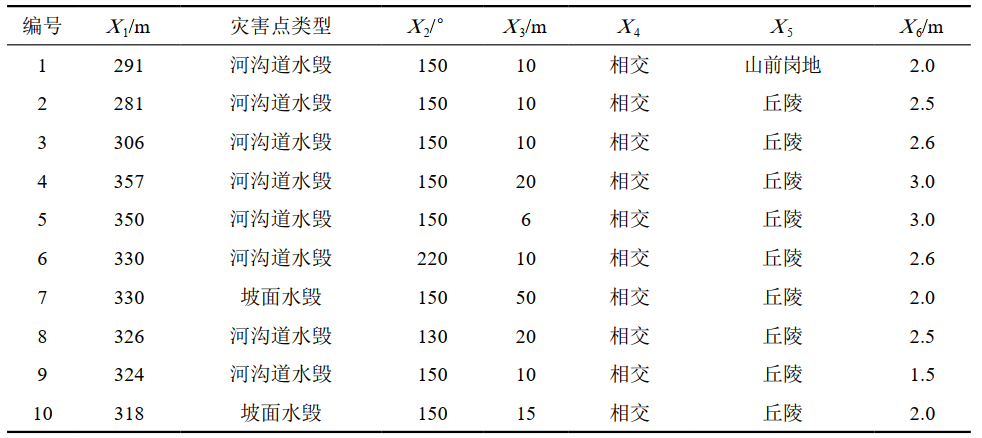
将原始数据在表格中进行整合，输入IBM SPSS Statistics中，经计算后将类别数据输出为量化数据，将SPSS输出结果带入易发性概率计算公式中，计算结果如表 5所示。

表 5 原始数据SPSS输出

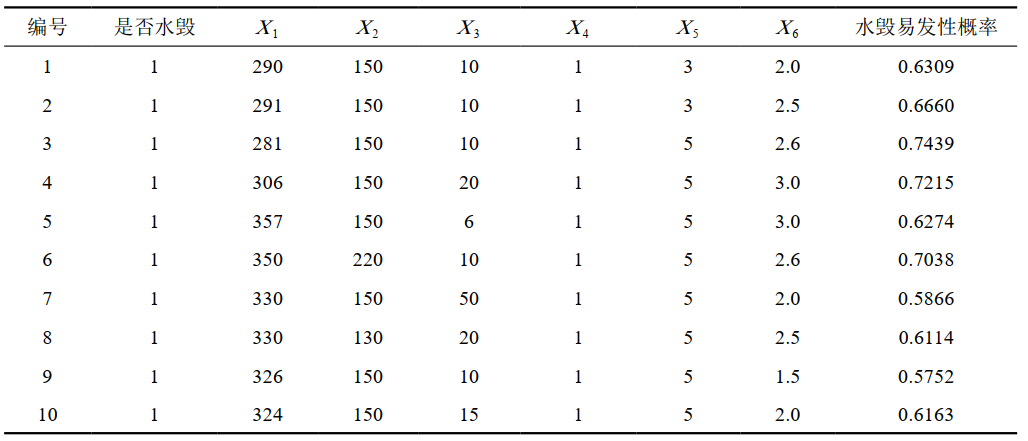
4  地质灾害易发区[5-6]划分

按照“区内相似、区际差异”的原则，即在同一类型的区内，地质环境背景条件、主要诱发条件和地质灾害发育特征应基本相似，而不同类型的区内，则具有明显的差异性。依据定量评价结果，借助GIS（地理信息系统）技术，用电子信息化手段合并易发性相同或者相近的概率单元格，对地质灾害易发性程度进行等级分区，分区主要特征如表 6所示。

表 6 地质灾害易发程度分区主要特征

5  总结与建议

（1）通过Logistic回归模型预测油气管道水毁地质灾害易发性概率效果较好，根据预测结果对易发程度分区，为管道地质灾害日常管理划出了重点，有利于管道管理单位将有限的资源合理利用，立足于治早治小，对油气管道水毁地质灾害防灾减灾有一定指导意义。

（2）由于地质灾害的发育是地质环境变化和影响因素综合作用的结果，是不断变化和发展的，在同一或临近区域的影响因素相似性高。因此本文介绍的关于Logistic回归模型水毁灾害易发性概率计算结果适用于长输油气管道的易发性分区。同时，该方法所需采集的样本较多，难以在日常管理中实施，主要依靠承包商单位周期性地质灾害专业化排查成果进行易发性预测分区。

（3）地质灾害的调查、防治将是一项长期的工作，下一步将结合区域监测预警信息，减少现场数据采集工作量，实现短周期地质灾害易发性分区，为长输油气管道的安全运营提供长期保障。

 

参考文献：

[1]田春山，刘希林，汪佳.基于 CF 和 Logistic 回归模型的广东省地质灾害易发性评价[J].水文地质工程地质，2016(11)：154-170.

[2]钟亩锋.基于确定性系数与Logistic回归模型的地质灾害易发性评价[J].世界有色金属，2020(01)：186-190.

[3]樊芷吟，苟晓峰，秦明月，范强，余建乐，赵建军.基于信息量模型与 Logistic 回归模型耦合的地质灾害易发性评价 [J].工程地质学报，2018(04)：340-347.

[4]钟荫乾.地质灾害易发性评价[J].湖北地矿，2002，16(4)：81-86.

[5]尚慧，倪万魁，程花.斜坡单元划分在彭阳县地质灾害危险性区划的应用[J].中国水土保持，2011，3(2)：48-50.

[6]苗雨.基于GIS和Logistic模型的地质灾害危险性区划研究[D].西安：长安大学，2010：1-59.

作者简介：何礼元，1995年生，2018年毕业于安徽理工大学地质工程专业，大学本科学历，助理工程师，主要从事长输油气管道地质灾害勘查、评估、监测预警工作。联系方式：13135548788，757279399@qq.com。