张皓 杨锋平 张良 吴峰

中国石油集团工程材料研究院有限公司

 

摘要：为确定输油气管道异型B型套筒可修复缺陷的合理尺寸范围，并确定B形套筒的最佳结构参数方案，采用有限元方法，针对Φ508 mm管道分析并建立了四种异型套筒构型，采用数值模拟方法验证不同构型设计的适用性，并基于应力分析结果给出了异型B型套筒优选方案。结果表明直线导角型和椭圆曲线型异型套筒应力分布结果最优，考虑到加工精度及参数检测难度，优先推荐直线导角型异型套筒工程应用。

关键词：异型B型套筒；构型设计；应力分析

 

输油气管道作为长距离输送原油和天然气的专用设施，是全球能源基础设施的重要组成部分，然而，管道在受到外载荷或腐蚀等影响时，可能形成服役安全隐患。在缺陷修复方面，目前国内外标准均规定其永久修复方式为B型套筒或换管。相比成本巨大的换管，B型套筒无疑是经济性与安全性的首选[1]。SY/T 7666―2022《油气管道缺陷修复用B型套筒》介绍，B型套筒修复技术是利用两个由钢板（或短节）制成的半圆柱外壳覆盖在管道缺陷处，且待修复管道缺陷轴向长度中心位于套筒长度的二分之一位置，两片套筒通过侧焊缝焊接在一起，套筒端部采用角焊的方式焊接在输送管道上。B型套筒的设计对其修复可靠性至关重要，套筒通常被设计成紧密地配合在管道的周围，提供安全稳定的支撑结构[2]。对于外载荷引起的管道大变形缺陷，如管体屈曲及褶皱缺陷，异型B型套筒是一种行之有效的修复方法，然而其结构形式及相关参数确定方法目前鲜有研究分析。基于异形B型套筒的基本结构特征，本文设计了4种异型套筒构型，基于应力分析结果给出了异型B型套筒优选方案。

1  套筒构型设计

1.1  套筒设计基础参数

为了修复管体屈曲、褶皱等大变形缺陷，异型B型套筒的基本结构为中间粗、两端细的圆筒状构型。根据变径段曲线不同形式，异型B型套筒基于4种构型进行了参数化设计，研究中采用三个长度参数（600 mm、800 mm、1000 mm）和五个可修复缺陷高度参数（5 mm、10 mm、15 mm、20 mm、37 mm）来分析均匀载荷下的应力分布。分析采用的被修复管道外径为508 mm。

变径段的曲线设计是本文研究的重点之一，根据曲线表达函数的不同，研究中将变径段分为一次曲线型、二次曲线型和高次曲线型。基于该思路，本研究设计了4种异型套筒构型：直线导角型、椭圆曲线型、抛物线型和Sigmond曲线型。以直线导角型异型套筒为例，套筒的截面形状被定义为几个不同的元素，即：直线段L1和L2；圆弧段R1和R2。每种异型套筒构型及关键尺寸等的详细说明见图 1～图 4。

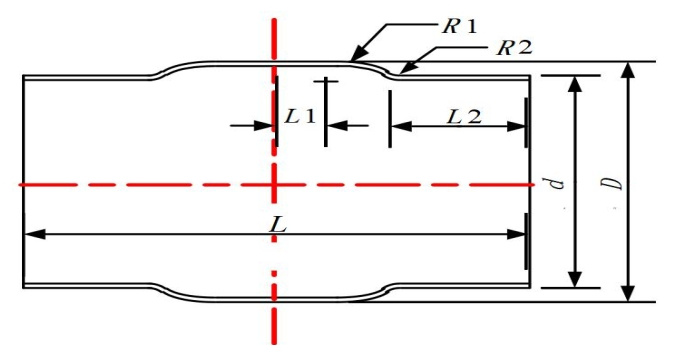
图 1 直线导角型套筒结构

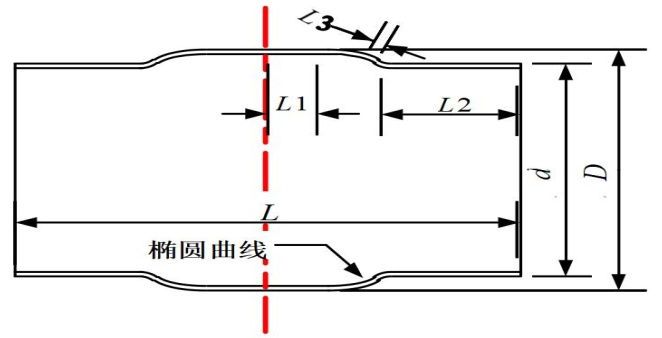
图 2 椭圆曲线型套筒结构

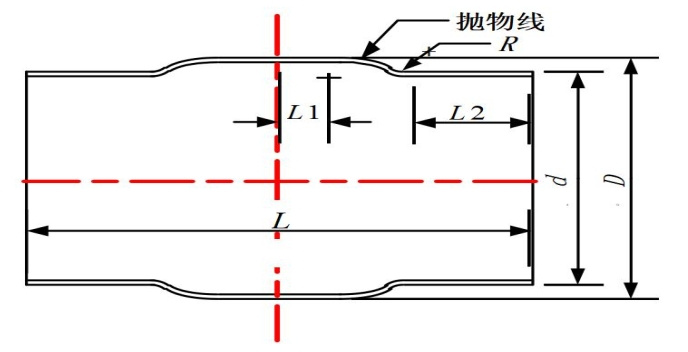
图 3 抛物线导角型套筒结构

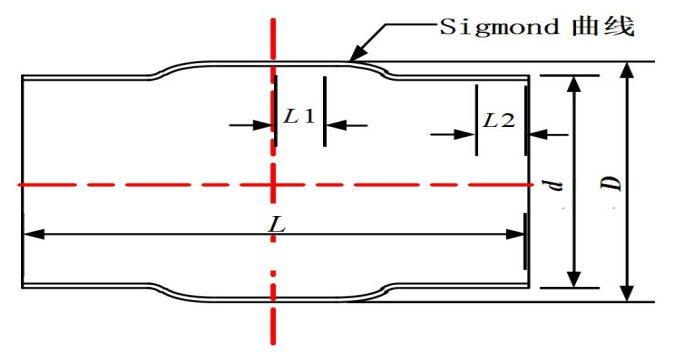
图 4 Sigmond曲线型套筒结构

图中根据套筒构型的不同分别设置一个初始的优化参数，即指定大径段、小径段的长度和各导角的半径。初始值的设置不影响最终的优化结果。

在获得4种套筒结构形式后，使用参数化建模工具Cero3.0软件生成四种不同套筒构型的分析模型，以便对这些模型进行有限元分析。计算及分析目的是优化各构型B型套筒的关键参数，最大限度地减少应力集中。

1.2  有限元模型

以直线导角型B型套筒为例，为了避免异形套筒的端部效应，套筒端部的长度延长到2.5 m。边界条件为远端两端面固结，管道及套筒内压载荷条件为8 MPa法向均压。结构评估以L长度上的应力集中水平为优化对象。以直线导角型B型套筒为例，优化前设置的初始尺寸如表 1所示。

表 1 直线导角型B型套筒优化初始参数

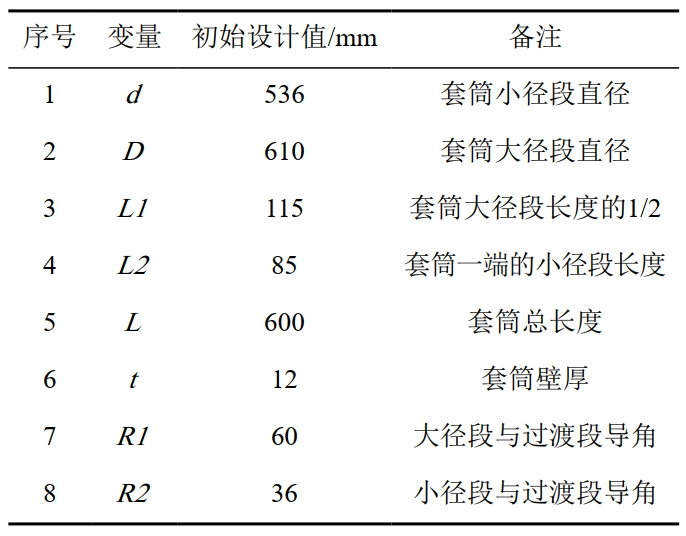
1.3  优化目标

本文的主要目标是找到满足以下条件的最佳套筒轮廓及其结构尺寸，计算中应满足以下条件：

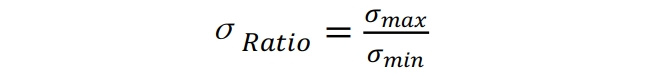
应力集中系数小于2；异形B型套筒的最大应力小于屈服强度的72%。

对于套筒的应力集中优化，选择四个目标函数，即：σRatio为应力集中系数=最大应力与最小应力之比；σmax为套筒段最大VonMises应力；σavg为套筒段的平均VonMises应力；σmin为套筒段最小VonMises应力。

2  应力计算与结果分析

2.1  设计空间

以直线导角型B型套筒为例，存在四个设计变量（L1、L2、R1、R2），每个变量取4个因子的初始设置值，以形成设计空间。本研究中涉及的异形B型套筒结构的设计考虑了各种因素对计算结果的影响，包括大径段长度L1、大径段与变径段导角R1、小径段长度L2和小径段与变径段导角R2。计算中采用控制变量法和正交实验法来减少模拟次数，通过对单个因素的模拟和数学模型的建立，研究了不同因素的影响规律，进而综合分析了多因素的影响，建立了统一的影响面和参数影响水平相关矩阵。利用不同参数组合的仿真结果对预测模型进行验证和改进，确保优化模型的可靠性。

在优化计算过程中，目标函数收敛误差小于0.1%。采样点选择使用中心复合设计方法，其中采样点由中心点、输入变量轴的端点和水平因子点组成。通过这种方法形成的部分因子样本点的数量随着设计变量的增加而增加，根据N=1+2n+（2n-f）计算（其中f是部分因子的数量，n是输入参数的数量，N是形成的样本点的数目）。总共需要计算25个模型。

根据相关修复标准中的推荐尺寸条件，其约束条件为：L1>110、L2>80、R1>60、R2>36。此外，空间几何图形约束的限制如下：

2.2  不同缺陷高度和套筒长度的异型套筒优化结果

经有限元计算分析，得出了各构型套筒的优化后参数。限于篇幅，本文给出了直线导角型和Sigmond曲线型的最终优化结果。

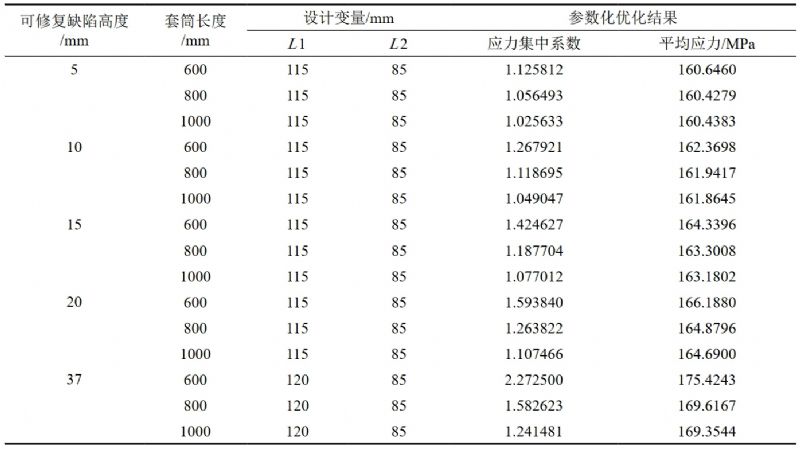
直线导角型套筒优化结果见表 2，优化结果表明，缺陷高度越大，应力集中系数越大，套筒应力储备裕度越小。表 3所示的计算结果表明，异型套筒可修复缺陷高度越大，套筒长度越小，应力集中系数越大，相应的套筒应力储备裕度越小。

表 2 直线导角型套筒优化结果

表 3 直线导角型套筒应力集中系数优化结果

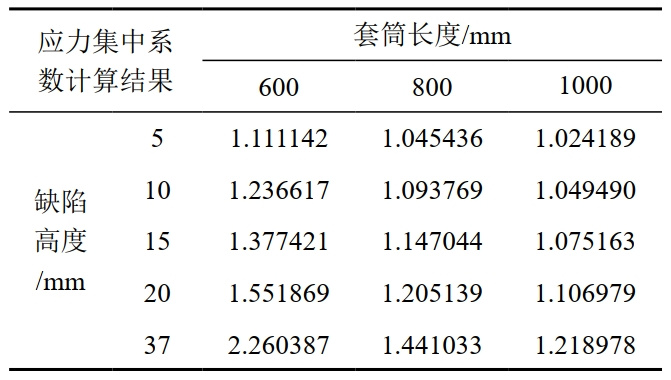
图 5说明了缺陷高度与套筒应力集中系数之间的关系。图中x轴表示以毫米为单位的缺陷高度，而y轴表示套筒应力集中系数。相同参数水平下的套筒应力分布结果比较表明，缺陷高度与套筒应力集中因子呈正相关，套筒长度与套筒应力集中因子负相关。此外，缺陷高度与套筒的最大VonMises应力呈正相关，而套筒长度则呈负相关。当缺陷高度保持不变时，较大的套筒长度下套筒应力集中系数较小，相应的应力储备裕度越大，反之亦然。

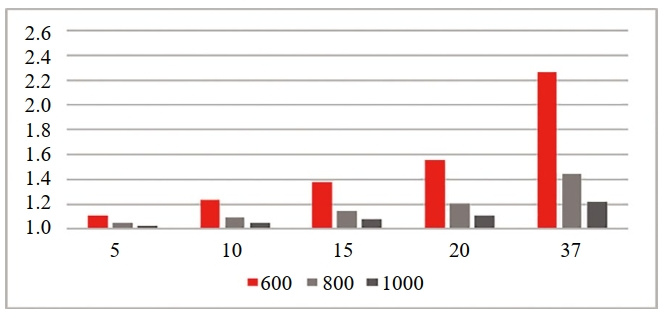
图 5 直线导角型套筒尺寸参数对应力集中系数的影响

Sigmond曲线型套筒优化结果，其结构尺寸根据相关修复标准中推荐的尺寸条件及其约束条件，确定设计变量L1>110、L2>80。此外，空间几何图形约束的限制如下：

L1+L2<L/2

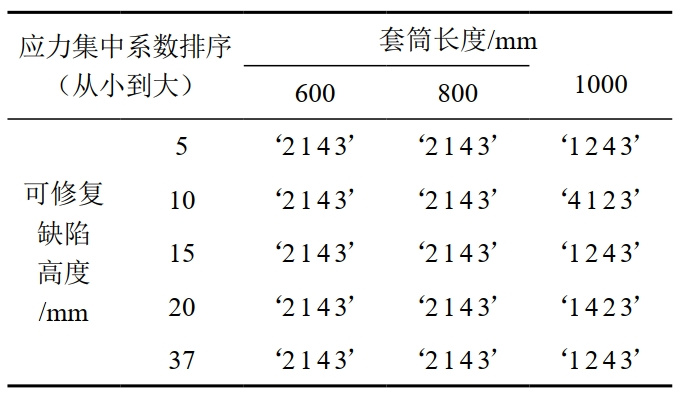
最终优化结果汇编见表 4。

表 4 Sigmond曲线型套筒优化结果（套筒长度 L=600 mm）

计算结果与直线导角型套筒类似，即缺陷高度越大，应力集中系数越大，套筒应力储备裕度越小。表 5所示的计算结果表明，Sigmond曲线型套筒可修复缺陷高度越大，套筒长度越小，应力集中系数越大，相应的套筒应力储备裕度越小。

表 5 Sigmond曲线型套筒应力集中系数优化结果

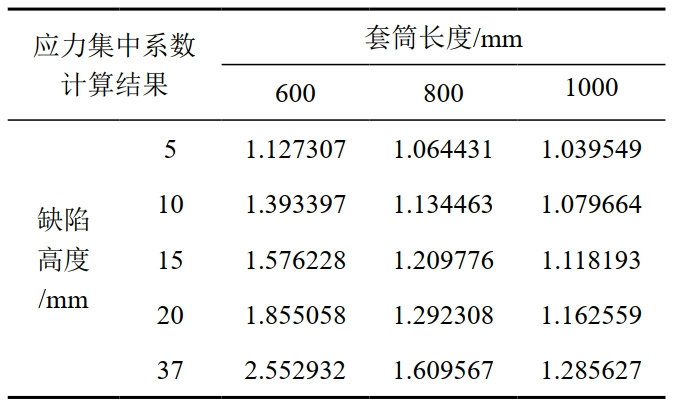
此外，图 6中所示的计算结果表明，应力集中因子随着缺陷高度的增加而增大，而随着套筒长度的增加而减小。此外，套筒的最大VonMises应力与缺陷高度呈正相关，与套筒长度负相关。

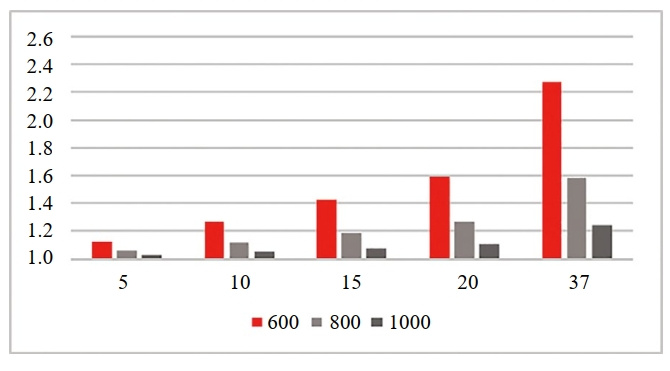
图 6 Sigmond曲线型套筒尺寸参数对应力集中系数的影响

综上，缺陷高度和套筒长度在决定套筒的应力集中系数、套筒应力储备裕度和最大VonMises应力方面起着重要作用。这项研究的结果表明了关键设计参数对异形套筒性能的影响，并为该类异型套筒选择合适的结构和可修复缺陷尺寸参数方案提供参考。

2.3  不同构型异型B型套筒优化结果

表 6中，1表示直线导角型套筒，2表示椭圆曲线型套筒，3表示抛物线导角型套筒，4表示Sigmond曲线型套筒。计算结果表明，当套筒长度为600/800mm时，椭圆曲线型应力集中因子最小，而当套筒长度为1000 mm时，直线导角型套筒应力集中因子最小。此外，椭圆曲线型在套筒长度为600/800 mm计算得到的最大应力值最小，而当套筒长度为1000 mm时，直线导角型/Sigmond曲线型套筒计算得到的最大应力值最小。

表 6 不同构型异型套筒优化结果及优选方案

3  结论

（1）基于变径段曲线不同形式，设计了4种不同构型的异型B型套筒，分别为直线导角型、椭圆曲线型、抛物线导角型和Sigmond曲线型。

（2）采用全参数化建模方法开展了各构型的异型套筒有限元计算，采用多目标遗传优化方法，对具有特定缺陷高度和套筒长度的异型B形套筒的设计变量参数进行了初始设置和边界条件限制，得到了合适的结构尺寸组合，以便提高计算效率并选出最优构型。

（3）设计了一系列可修复缺陷高度和套筒长度以进行对比分析，每种构型的异型套筒均计算了5种缺陷高度和3个套筒长度下的应力分布。结果表明，当套筒长度为600/800 mm时，椭圆曲线型套筒应力分布结果最优；当套筒长度为1000 mm时，直线导角型套筒应力分布结果最优。

（4）从工程应用方面考虑，建议异型套筒加工时优先选用直线导角型套筒，加工难度相对较小，且关键尺寸更易控制和检测；可将椭圆曲线型套筒作为备选方案，待加工及测量条件允许时再行应用。

 

参考文献：

[1]Wang, Y., Zhang, Y., Zhang, J., & Li, X. A study of the mechanical behavior of B-type sleeves for oil pipelines. Journal of Petroleum Science and Engineering, 145, 20-28. 2016.

[2]Li, X., Wang, Y., Zhang, Y., & Zhang, J. A review of B-type sleeves for oil pipelines. Journal of Pipeline Engineering, 17(1), 1-10. 2018.

作者简介：张皓，1990年生，毕业于西安交通大学航天学院，高级工程师，现从事油气输送管道及站场设备安全评价及失效分析研究。联系方式：15829616623，zhanghao6@cnpc.com.cn。